Emmanuel Betranhandy, Nathalie Vast and Jelena Sjakste
The mechanical properties of boron carbide at high pressure, explained from first principles.
By theoretical methods based on the density functional theory (DFT and DFPT) [1] [2], the physical properties of boron carbide have been studied for different carbon concentrations and versus temperature and pressure. A type of defect is identified, whose appearance at high pressure and high temperature, can explain the poor mechanical strength upon impact of the material . These results point the way to synthesize a superconducting material combining good mechanical strength at high pressure.
The boron carbides are a class of materials of industrial interest due to their outstanding mechanical properties, including very high hardness and excellent wear resistance, making them materials of choice for cutting tools. They also exhibit good resistance to compression, but their use as materials for protection against mechanical impact is limited by low resistance to shock waves greater than 40 GPa. [3]
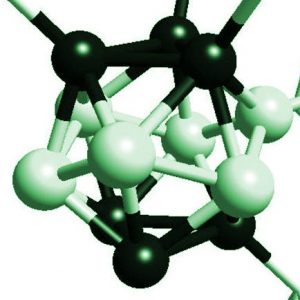
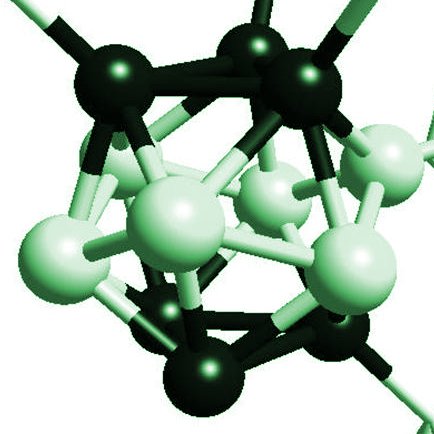
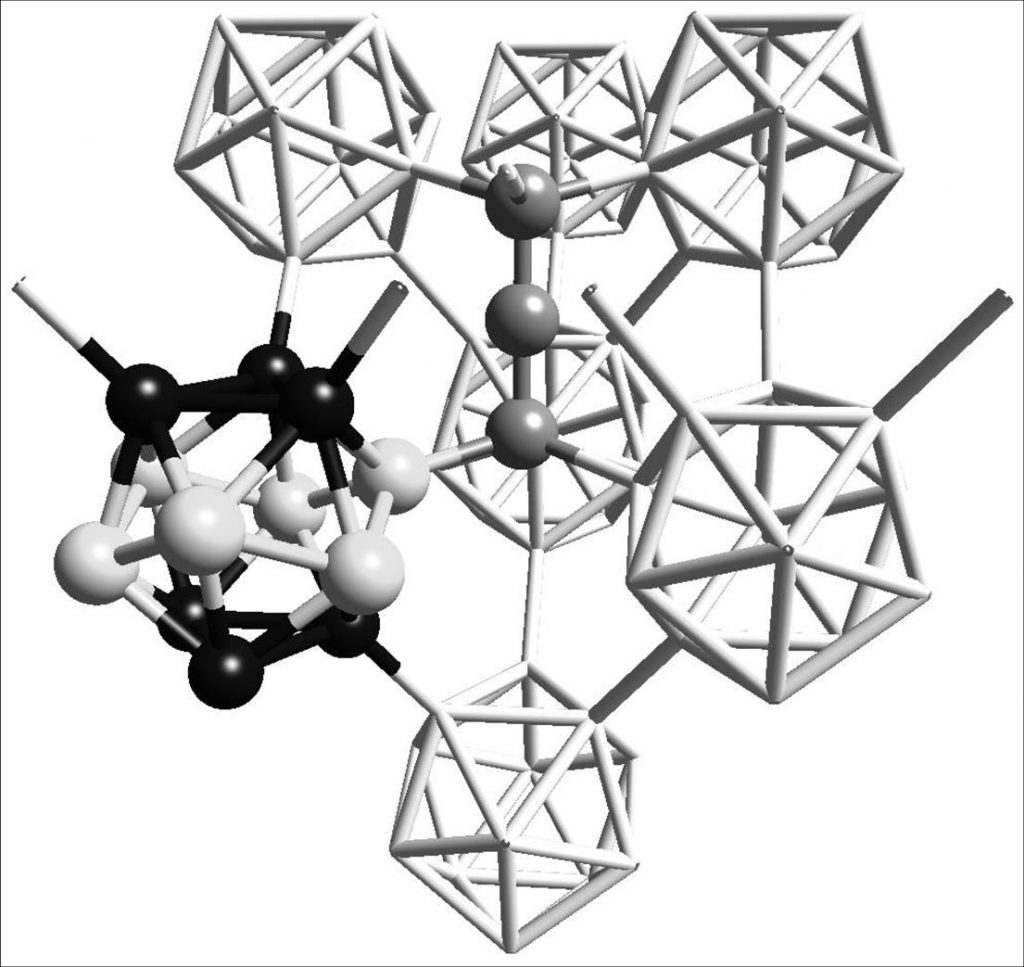
The atomic structure of boron carbide B4C is based on an assembly of icosahedra made of 12 atoms. These icosahedra are necessarily distorted because the 5-fold symmetry operations of the icosahedron are incompatible with any periodic translational symmetry of the crystal. These icosahedra are bounded each other either directly or through triatomic channels (Figure 1). The precise structure of the carbon-rich boron carbide (20% at. carbon) could not be determined experimentally, because of various difficulties. We have then studied the total energy obtained by DFT and the spectra of atomic vibrations for various models of atomic structure [4,5]. These studies show that the atomic structure of B4C is formed of C-B-C chains bounding the vast majority of B11C icosahedra, and some percent of icosahedra B10C2. Carbon atoms are located in the polar site of the icosahedron (B4Cp) (Figure 1).
Figure 1: Atomic structure of icosahedral boron carbide of Ref. [4]. Seven distorted icosahedra are shown. The vectors of the Bravais lattice (not shown) link the centers of icosahedra. The black balls are the atoms in polar site p. The gray balls are the atoms in equatorial site. The dark gray spheres represent the atoms at the center and the ends of the triatomic chains. An atom in polar site is directly bounded to a polar atom of another icosahedron by a covalent p-p bond similar to the covalent bonds in diamond. An atom in an equatorial site is bound to a carbon atom at a chain end.
With the aim of understanding the poor mechanical strength of boron carbide under shock waves beyond 40 GPa, we explored by DFT the stability of many carbides of boron B4Cp with different carbon concentrations, slightly above 20%. These compounds are obtained from the B4Cp by introducing defects (boron vacancies). Calculations show that the majority of these compounds are unstable and decompose into boron + graphite [6]. However, for one of the compositions, a phase transition under pressure can be evidenced, which does not occur in B4Cp. Moreover, the transition pressure is in agreement with the experimental pressure [3] at which the shock wave induces the change of resistance of the material . The generation of metastable defects during the passage of the shock wave, is at the origin of the observed transition, and is therefore responsible for the poor mechanical strength of the icosahedral boron carbide at high pressure [7].
In conclusion, the idea of combining high hardness and superconductivity in the same material by doping the boron carbide has recently emerged. Indeed, calculations have shown that doping of boron carbide B4C through holes is a path of choice for conventional superconductivity. The strength of the electron-phonon coupling in B13C2 is of the same order of magnitude as that of the superconductor MgB2 [8]. By combining our knowledge of superconductivity in these materials and of their mechanical strength at high pressure, would allow to design a superconductor material with high mechanical strength under impact.
References:
[1] Tutorial by Walter Kohn, Nobel Price of Chemistry 1998 :
“Electronic Structure of Matter – Wave Functions and Density Functional“
[2] S. Baroni, S. de Gironcoli, A.D. Corso, and P. Giannozzi, Rev. Mod. Phys. 73, 515 (2001).
[3] F. Mauri, N. Vast and C.J. Pickard, Phys. Rev. Lett., 87, 085506 (2001).
[4] R. Lazzari, N. Vast, J.M. Besson, S. Baroni and A. Dal Corso, Phys. Rev. Lett. 83, 3230 (1999); Ibid 85, 4194 (2000).
[5] T. J. Vogler, W. D. Reinhart, and L. C. Chhabildas, J. Appl. Phys. 95, 4173 (2004).
[6] N. Vast, J. Sjakste and E. Betranhandy, J. Phys.: Conf. Ser. 176 012002 (2009).
[7] M. Calandra, N. Vast and F. Mauri, Phys. Rev. B 69, 224505 (2004).
[8] E. Betranhandy, N. Vast, and J. Sjakste, in preparation (2009).