Dans leurs principes, nos outils technologiques modernes s’appuient très largement sur des résultats de recherches fondamentales en physique de la matière condensée : semi-conducteurs, jonctions, diodes, lasers, magnéto-résistance géante… Pour préparer les applications de demain, ces recherches tentent aujourd’hui de trouver et de décrire de nouveaux états de la matière, allant au-delà des situations « classiques », où se manifestent des comportements quantiques. Les glaces de spin, milieu ferromagnétique s’aimantant à basse température selon des structures similaires à celle de la glace d’eau, et leurs analogues quantiques sont des exemples de tels systèmes [1].
Un travail, réalisé dans le cadre d’une collaboration avec les équipes du Laboratoire Léon Brillouin, donne quelques clefs pour comprendre la physique de ces glaces de spin. Une analyse fine des données expérimentales permet de relier les contraintes aléatoires induites par l’infime désordre chimique du matériau au spectre des fluctuations magnétiques, observé par diffusion inélastique des neutrons. Le modèle développé à l’occasion de ce travail expérimental ouvre la voie au contrôle par cristallogenèse des corrélations des fluctuations quantiques, en montrant leur lien quantitatif avec le désordre structural [2].
La structure cristallographique usuelle des « glaces de spin » est basée sur un réseau de type « pyrochlore », formé d’un ensemble de tétraèdres connectés par leurs sommets (Fig. a), chaque nœud étant occupé par un ion de terre rare magnétique : Tb, Dy, Ho, Pr…. Dans ces composés, les orbitales électroniques de valence ont une forme très allongée en direction du centre de chaque tétraèdre. Le moment magnétique, ou spin, de chaque ion ne peut alors pointer que vers l’intérieur ou vers l’extérieur d’un tétraèdre, à l’instar des états ±1 d’une variable de type « Ising ». L’état fondamental classique d’un tel système est très particulier car infiniment dégénéré. En effet, la seule prescription pour le construire est de suivre une règle locale qui stipule que chaque tétraèdre doit comporter deux spins « in » qui pointent vers l’intérieur et deux spins « out » qui pointent vers l’extérieur. Ces configurations « 2 In – 2 Out » sur chaque tétraèdre forment l’analogue des liaisons H courtes et longues bien connues dans la glace d’eau, d’où ce nom de « glace de spin ».
Ces dernières années, une vision nouvelle du problème a été proposé en remarquant que la règle « 2 In-2 Out » est en fait analogue à la loi de conservation du flux en électromagnétisme, selon l’équation de Maxwell : ∇B = 0 [3]. L’analogie est complète dès lors qu’on incorpore les fluctuations quantiques. En effet, les fluctuations du champ magnétique fictif B, créent un champ électrique « émergent » E. Ainsi, selon les prédictions théoriques, une glace de spin quantique devrait comporter un spectre d’excitation particulier caractérisé par un mode analogue au photon de l’électromagnétisme.
Mais comment approcher ce problème ? L’idée est de créer une glace de spin où l’ion magnétique serait doté de nouvelles propriétés. C’est par exemple le cas de Pr2Zr2O7 [4]. L’orientation du spin de l’ion magnétique praséodyme Pr3+ présente la particularité d’être extrêmement sensible aux infimes contraintes structurales aléatoires, inévitables dans tout matériau macroscopique. Tout se passe alors comme si le désordre faisait fluctuer le spin entre les états d’Ising ±1, de façon similaire aux fluctuations quantiques dans l’analogie électromagnétique (voir aussi [5] et [6]).
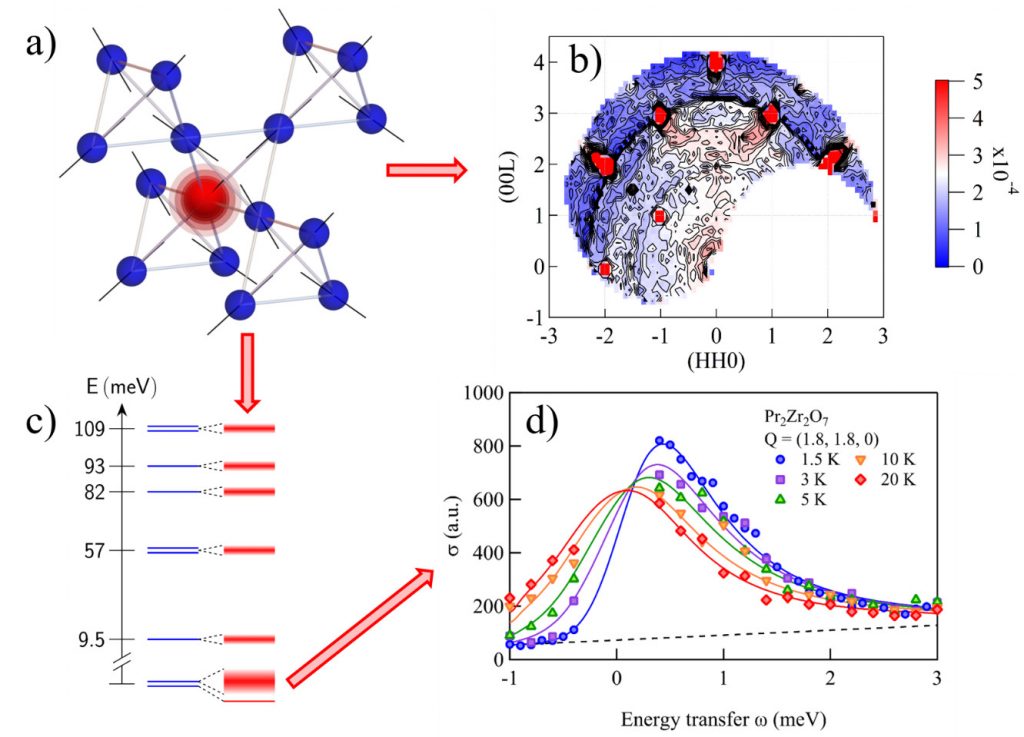
a) Structure « pyrochlore » du composé Pr2Zr2O7. Les sphères bleues représentent les ions magnétiques Pr3+. La sphère rouge matérialise un ion Zr se substituant localement au Pr et induisant une contrainte locale sur la structure du matériau.
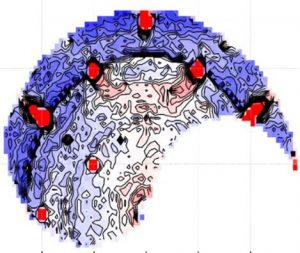
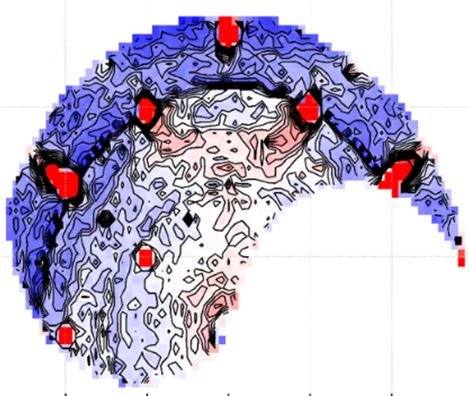
b) Carte de diffusion diffuse de neutrons révélant les infimes distorsions du réseau liées aux inversions Pr ↔ Zr.
c) Spectre de fluctuations magnétiques des ions Pr3+ en l’absence (bleu) ou en présence (rouge) de contraintes.
d) Spectre de diffusion inélastique de neutrons (symboles) décrits par un modèle prenant en compte la présence de défauts (traits pleins, obtenus sans paramètre ajustable)
Afin de clarifier ce point crucial, une série de mesures de diffusion élastique de neutrons polarisés a été réalisée sur l’instrument D7 de l’Institut Laue Langevin (ILL, Grenoble), permettant de déterminer de manière très précise les propriétés structurales fines de Pr2Zr2O7, inaccessibles à toute autre technique de caractérisation. Il est ainsi possible d’évaluer l’ampleur réelle du désordre présent dans l’échantillon, en modélisant l’intensité détectée autour des pics de Bragg de la structure « parfaite » par un modèle de diffusion « Huang », habituellement employé pour décrire les champs de déplacement induits dans des alliages métalliques par irradiation d’électrons de haute énergie (Fig. b). Le résultat de cette analyse offre une estimation directe de l’infime proportion (de l’ordre de 1 ‰) de sites du réseau sujet à des perturbations. De plus, les contraintes associées à ces défauts peuvent être évaluées, ainsi que leur impact sur les fluctuations de spin. De façon schématique, l’effet principal de ces contraintes est d’autoriser l’apparition d’un spectre de transitions magnétiques (voir le schéma de la Fig. c), dont l’énergie est distribuée selon une loi prédite par un modèle théorique développé conjointement aux expériences [2]. Ce spectre de diffusion inélastique de neutrons, mesuré sur le spectromètre 4F1 du Laboratoire Léon Brillouin (Saclay), peut être parfaitement décrit par le modèle développé (voir Fig. d). Cette correspondance remarquable entre théorie et expérience valide de fait le lien entre désordre et dynamique de spin.
La conclusion de cette étude approfondie du composé Pr2Zr2O7 est qu’il est désormais possible de relier le désordre chimique aux propriétés dynamiques des glaces de spin, par l’utilisation conjointe d’outils expérimentaux et théoriques adéquats. Cette approche permet de proposer une méthode pour maitriser les fluctuations quantiques dans les matériaux considérés et constitue une étape fondamentale en vue de la réalisation d’une glace de spin quantique.
Références :
[1] « Quantum spin ice: a search for gapless quantum spin liquids in pyrochlore magnets »
M.J.P. Gingras and P.A. McClarty, Rep Prog Phys 77 (2017) 056501.
[2] « Disorder and Quantum Spin Ice »
N. Martin, P. Bonville, E. Lhotel, S. Guitteny, A. Wildes, C. Decorse, M. Ciomaga Hatnean, G. Balakrishnan, I. Mirebeau and S. Petit, Phys Rev X 7 041028 (2017).
[3] « Magnetic monopoles in spin iceSpin Ice »
Castelnovo, C. and Moessner, R. and Sondhi, S. L., Nature, 451, 42 (2008).
[4] “Quantum fluctuations in spin-ice-like Pr2Zr2O7”
K. Kimura, S. Nakatsuji, J.-J. Wen, C. Broholm, M.B. Stone, E. Nishibori and H. Sawa, Nature Communications 4, 1934 (2013)
[5] « Disordered Route to the Coulomb Quantum Spin Liquid: Random Transverse Fields on Spin Ice in Pr2Zr2O7«
J.-J. Wen, S.M. Koohpayeh, K.A. Ross, B.A. Trump, T.M. McQueen, K. Kimura, S. Nakatsuji, Y. Qiu, D.M. Pajerowski, J.R.D. Copley and C.L. Broholm, Phys Rev Lett 118, 107206 (2017).
[6] « Disorder-Induced Quantum Spin Liquid in Spin Ice Pyrochlores »
L. Savary and L. Balents, Phys Rev Lett 118, 087203 (2017).
Contact CEA : Sylvain Petit, Laboratoire Léon Brillouin / Groupe « Nouvelles Frontières des Matériaux Quantiques« , CEA Saclay.
Collaboration :
- S. Guitteny, N. Martin, I. Mirebeau & S. Petit : Équipe NFMQ, Laboratoire Léon Brillouin, UMR 12, CEA-Saclay, CEA, CNRS, 91191 Gif-sur-Yvette Cedex, France
- P. Bonville : Service de Physique de l’Etat Condensé, UMR 3680, CEA-Saclay, CEA, CNRS, 91191 Gif-sur-Yvette, France
- E. Lhotel : Institut Néel, CNRS et Univ. Grenoble Alpes, 38042 Grenoble, France
- A. Wildes : Institut Laue Langevin, 38042 Grenoble, France
- C. Decorse : ICCMO, Université Paris-Sud, 91405 Orsay
- M. Ciomaga Hatnean & G. Balakrishnan : Department of Physics, University of Warwick, Coventry CV4 7AL, Royaume-Uni .