Among the many novel phenomena encountered in strongly-correlated electron systems, specific effects originating from the interplay of different degrees of freedom (lattice, electron charge, spin and orbital angular momentum) have aroused particular interest. One prominent example is the manganites, which are well known for their colossal magnetoresistance (CMR) properties, associated with a phase transition from a high-temperature insulating phase to a low-temperature metallic phase [1].
In these perovskite manganese oxides La1-xBxMnO3 (B = Ca, Sr), the number of electrons on each manganese ion can be tuned by the partial substitution of a concentration x of Ca or Sr atoms on the La site. For x = 0, there are 4 electrons per manganese site, whose spins are aligned because of a large Hund coupling. The system shows orbital ordering, owing to the Mn3+ Jahn-Teller effect, and is insulating as a result of electronic correlations. In agreement with the Goodenough-Kanamori rules, the spins form ferromagnetic planes that are stacked antiferromagnetically. Upon substitution, the number of electrons per manganese site decreases and the system evolves towards an orbitally disordered ferromagnetic and metallic phase beyond x ≈ 0.17. The latter phase is the one exhibiting the famous CMR properties. The hopping of electrons from site to site leads to a novel type of ferromagnetic coupling (“double exchange”), which is expected to stabilize the ferromagnetic order. However, the way the material evolves towards this new phase is very peculiar and emphasizes the role of charge segregation. The signature of this evolution was characterized by means of inelastic neutron scattering experiments in the course of of a longstanding collaboration with the State Steel and Alloys Institute in Moscow (MISIS).
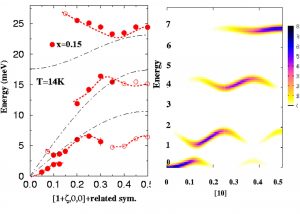
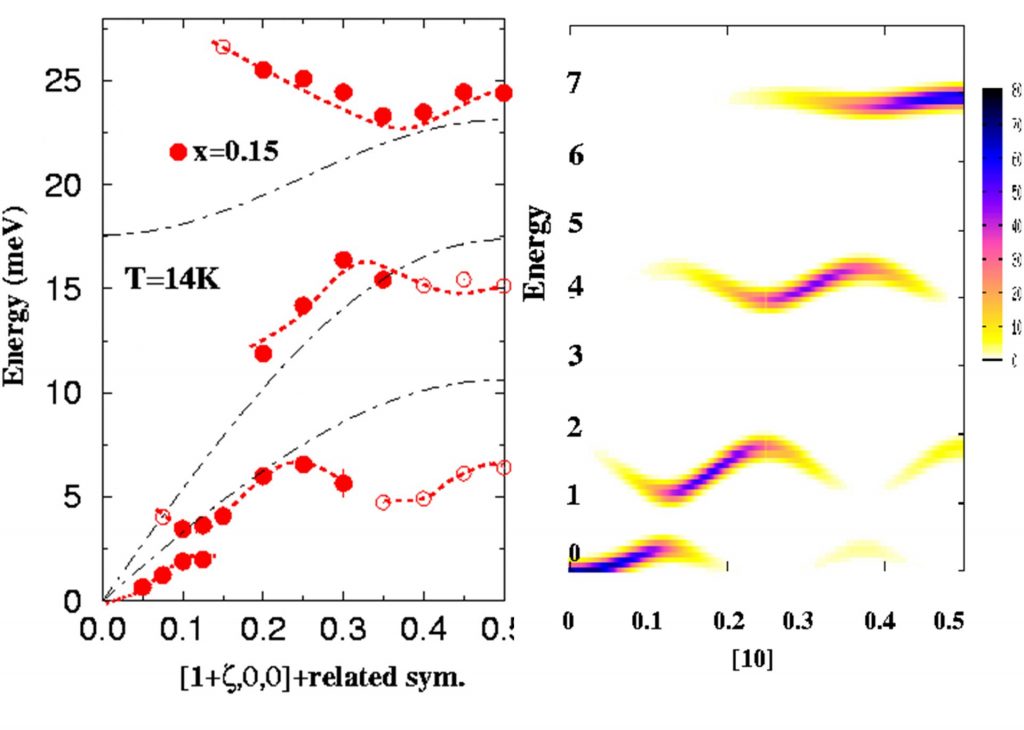
We first showed that, for small x values, the electronic state can be seen as consisting of hole-rich platelets embedded in a hole-poor matrix within the ferromagnetic planes. Their size (~16 Å) and spatial extension could be determined. As x increases, these platelets grow and percolate for x = 0.12, where the antiferromagnetic coupling between layers vanishes [2][3][4][5]. The system becomes quasi-metallic at room temperature but, in a small range of concentrations around x ~1/8, the ground state remains insulating owing to charge localization. Our study in this regime revealed very unconventional spin dynamics: the magnetic excitation spectrum consists of a dispersive branch near the zone centre, and several discrete modes at the zone boundary [6]. The former indicates long-range ferromagnetically coupled spins, while the latter were attributed to standing spin waves within small ferromagnetic domains. By assuming that the system forms weakly-coupled ferromagnetic clusters, we were able to explain the data successfully, and to obtain a very good agreement between the expeiment and the model (Figure 1).
[1] Nanoscale Phase Separation and Colossal Magnetoresistance, edited by E. Dagotto (Springer-Verlag, Berlin, 2002).
[2] M. Hennion et al., Phys. Rev. Lett. 81 1957 (1998).
[3] M. Hennion et al., Phys. Rev. B 61, 9513 (2000).
[4] F. Moussa et al., Phys. Rev. B 67, 214430 (2003).
[5] M. Hennion et al., Phys. Rev. Lett. 94 057006 (2005)
[6] M. Hennion et al., Phys. Rev. B 73, 104453 (2006)
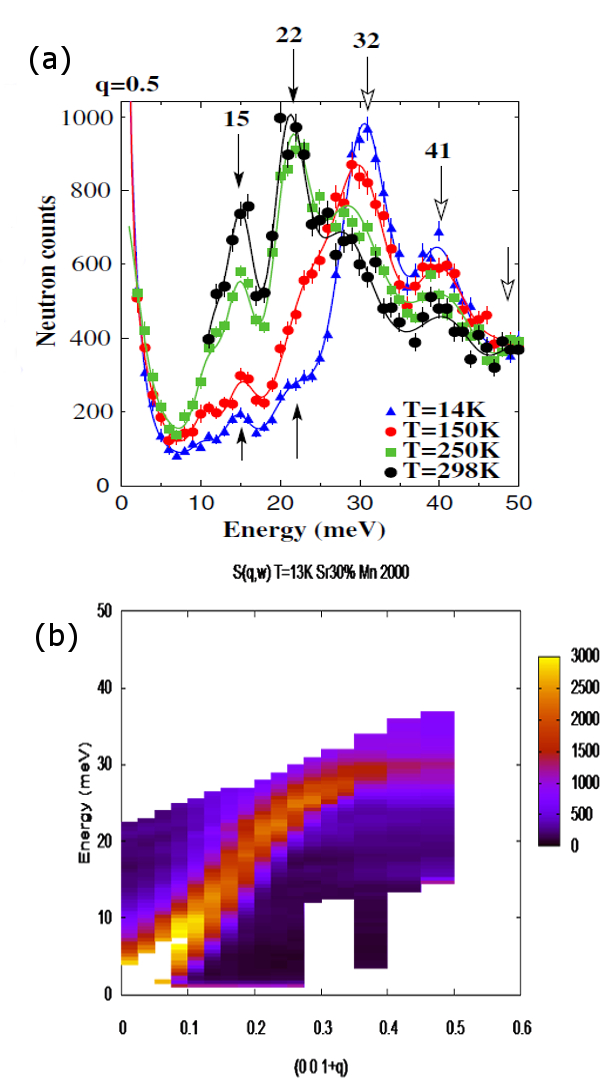
Beyond x = 0.17, the system enters the ferromagnetic and metallic phase. Pioneering measurements revealed standard cosine laws, although with strong anomalies at the zone boundary, which were described in terms of softening, broadening and flattening of the dispersion. These anomalies were tentatively explained on the basis of a phenomenological Heisenberg model with Mn-Mn magnetic couplings extending up to the fourth neighbors. Subsequently, we revisited these experiments with improved statistics and resolution, and collected data for a number of doping contents (x(Sr) = 0.175, 0.2, 0.3, 0.35 0.4 and x(Ca) = 0.3) [1][2][3][4]. We found that in all cases the spin-wave spectra consisted of a quadratic dispersive branch at the zone centre, characteristic of a three-dimensional (3D) ferromagnetic state, and wave-vector independent (flat) levels at the zone boundary, which were reminiscent of the x ~1/8 spectra. The characteristic energies of these levels remain approximately identical, while their intensities show a peculiar temperature and doping dependence. Actually, as the temperature decreases or x increases, the upper modes become very intense at the expense of the lower ones (Figure 2a). At low temperature, this creates the illusion of a cosine law (the quadratic branch) with a softened zone boundary (the upper flat mode), which is in agreement with earlier reports (Figure 2b). It is worth emphasizing that, as soon as temperature increases, this effect vanishes as all modes have comparable intensities. Considering the resemblance between the spectra in the x ~1/8 region and in the metallic phase, it is tempting to propose a picture where the levels would reflect quantized spin waves in ferromagnetic clusters, embedded in a 3D ferromagnetic matrix. As both insulating and metallic regimes have similar spin-wave spectra, we may speculate that the same physics is at play here and that the existence of such clusters is an important ingredient for the appearance of the CMR phenomenon. However, the stability of these clusters for doping as large as x = 0.35 or 0.40 is probably difficult to justify, and casts some doubt on the proposed interpretation. Up to now, the unconventional spin dynamics remain unexplained and new experimental efforts are needed to extend our understanding of these compounds and their puzzling properties.
The bilayer counterpart of the pseudo-cubic manganites, La2-2xSr1+2xMn2O7, is also famous for its colossal magnetoresistance. Here, broad charge-order peaks due to large polarons are found to disappear at the CMR insulator-metal transition. These polarons survive as fluctuations in the metallic phase, which strongly broaden and soften certain phonon modes near the wave-vectors where the charge-order peaks appeared in the high-temperature phase [5]. Again, these findings confirm the amazing entanglement of lattice, charge and spin degrees of freedom in this class of systems.
[1] F. Moussa et al., Phys. Rev. B 76, 064403 (2007)
[2] Intralayer and interlayer exchange tuned by magnetic field in the bilayer manganite (La0.4Pr0.6) 1.2Sr1.8Mn2O7 probed by inelastic neutron scattering
F. Moussa, M. Hennion, A. Gukasov, S. Petit, L. P. Regnault, A. Ivanov, R. Suryanarayanan, M. Apostu, and A. Revcolevschi, Phys. Rev. B 78, 060406 (2008).
[3] Spin waves and metallic state of magnetoresistive manganites
S. Petit, M. Hennion, F. Moussa, D. Lamago, A. Ivanov and Y.Mukovskii, J. Phys. Conf. Ser. 200, 012159 (2010).
[4] Quantized Spin Waves in the Metallic State of Magnetoresistive Manganites
S. Petit, M. Hennion, F. Moussa, D. Lamago, A. Ivanov, Y. M. Mukovskii and D. Shulyatev, Phys. Rev. Lett. 102, 207201 (2009).
[5] Signature of checkerboard fluctuations in the phonon spectra of a possible polaronic metal La1.2Sr1.8Mn2O7
F. Weber, N. Aliouane, H. Zheng, J. F. Mitchell, D. N. Argyriou & D. Reznik, Nature Materials 8, 798 (2009).