Electric field switching of Rashba splitting using ferroelectric polarization
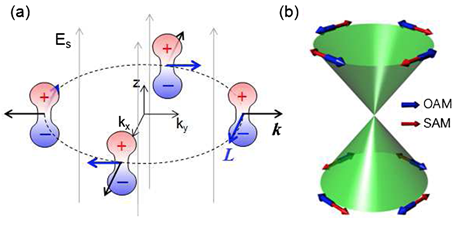
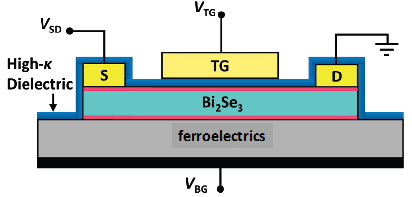
The ambition of our work is to control spin-orbit coupling in an emerging class of spintronics materials, such as topological insulators and their parent compounds, deposited on thin films ferroelectric (FE) substrate (Figs. 1, 2 and 3). One of the most interesting and useful features of FE materials is the strong coupling of the polarization with elastic strain that can be switched by an external electric field. The remnant polarization in a FE should provide a robust and reproducible control of the Rashba-type electron band spin splitting in a 2D system and therefore potentially of spin transport properties.
Experimental and theoretical studies within the project will be closely matched to obtain valuable information on spin polarisation and contribute to providing a framework for new type of applications in spintronics.
|
|
|
|
|
|
|
Figure 1: a) Interaction of the electric dipole moment and surface electric field Es, and resulting alignment of the orbital angular momentum (OAM). |
|
Figure 2: Scheme of a back-gated/top-gated device. The top and bottom TI surface states are indicated by red lines. |
|
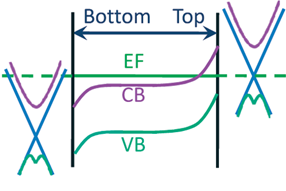
Figure 3: Schematic variation of the band structure along the vertical direction, showing the bulk conduction (purple) and valence (green) bands bending. The TI states bands (light blue) can be shifted by application of a gate voltage. |
Topological Insulators
Topological insulators (TI) are new states of quantum matter in which surface states residing in the bulk insulating gap of such systems are protected by time-reversal symmetry ([HAS10], [Qi11]). The electronic band structure of these materials includes characteristic conical features at high-symmetry points within the Brillouin zone. Electrons in the vicinity of a cone exhibit linear dispersion and are expected to behave like massless Dirac fermions confined within a two-dimensional plane (Fig. 4).
The transport properties of a topological insulator are closely related to the two-dimensional (2D) integer quantum Hall effect, which also has unique edge states. These electronic states are insensitive to disorder because there are no states available for backscattering. They were originally predicted to exist in graphene [Kan05, Ber06]. Graphene is made out of carbon, which is a light element with a weak spin-orbit interaction. Clearly, a better place to look for this physics would be in materials with strong spin-orbit interactions, made from heavy elements near the bottom of the Periodic Table.
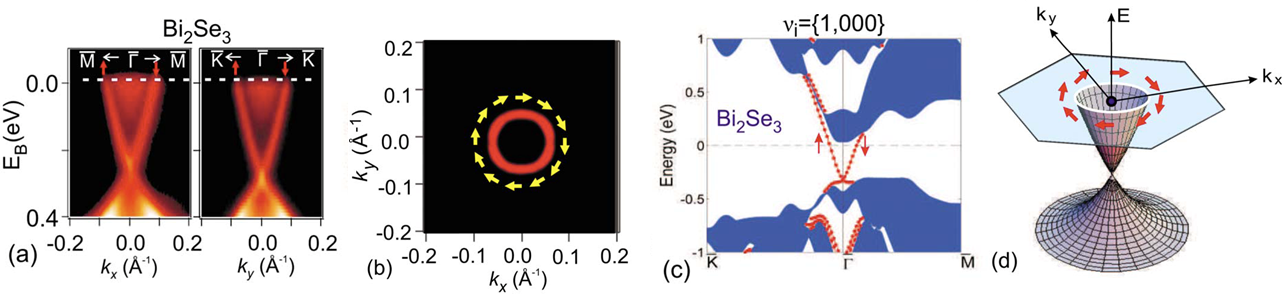
Figure 4: Spin-momentum locked helical surface Dirac fermions are hallmark signatures of topological insulators. a) ARPES data for Bi2Se3 reveal surface electronic states with a single spin-polarized Dirac cone. b) The surface Fermi surface exhibits a chiral left-handed spin texture. c) Surface electronic structure of Bi2Se3 computed in the local-density approximation. The shaded regions describe bulk states, and the lines are surface states. d) Schematic of the spin-polarized surface-state dispersion in Bi2X3 (1;000) topological insulators.
From: [Has10]
Topological Insulators: Thin films
Whereas the surfaces of bulk topological insulators provide a promising basis for spintronics application, thin films are more relevant for actual device architecture. Effort has been made to reduce the thickness of known bulk topological insulators. The choice of available materials is thus substantially broadened. However, the usable film thickness has a natural lower limit, below which the two film boundaries may be coupled by quantum tunnelling, so that a small, thickness-dependent gap opens up at the Dirac point, cutting off the spin conduction.
Thin film parent compound of topological insulators
The requirement of fine-tuning the thickness makes the experimental fabrication of 2D topological insulators rather difficult. Therefore, it is desirable to search for new materials or new schemes to obtain a 2D topological insulator. The Bi(111) film on a suitable substrate actually represents a special interesting class of films having an intermediate inter-bilayer (BL) coupling strength that may have a significant influence on the topological property [Liu11]. It should be noted that the substrate may have additional effects on the electronic structure and hence the topological properties of Bi films, which are of central interest for these studies.
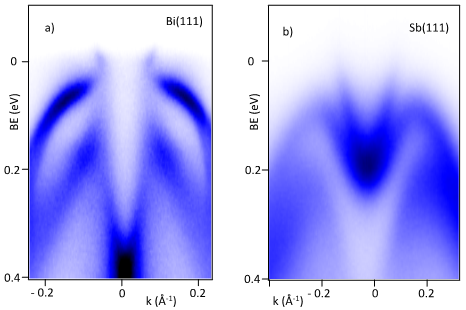
Figure 5: ARPES spectra of: a) (111) face of a Bi monocrystal (12 ML) prepared on a InAs(111)-A face; b) (111) face of a Sb monocrystal prepared on a Bi(111) buffer layer shown in a).
We have extensive experience with thin layer growth. Bi growth is epitaxial and a Bi monocrystal of very high quality is obtained after depositing several monolayers (Fig. 5a). The band dispersion fits well with literature data on Bi single crystals [Hof06, Hir06]. On top of Bi(111) we were able to prepare high quality Sb(111) monocrystals (Fig. 5b). The Sb(111) and the Bi(111) surfaces have a hexagonal structure; their lattice constants are 4.30 and 4.54 Å, respectively; so the lattice mismatch is ~5% for Sb grown on a Bi buffer layer.
Theoretical description
This part of the work will be done in close collaboration with our colleagues from Ludwigs-Maximilians-Universität, Munich, Germany. The interpretation of the spin dependent band structure, as observed in ARPES, will be supported by ab-initio Korringa-Kohn-Rostoker (KKR) electronic structure calculations which account for all aspects of the investigated TIs: spin-orbit coupling without approximations by a fully relativistic approach, interdiffusion and disorder by means of the coherent potential approximation (CPA) and correlations by the dynamical mean field theory (DMFT). For this the layer dependent spin texture, as well as the spin and orbital resolved Bloch-spectral function will be determined. The measured ARPES spectra will be complemented by calculations on the basis of the one-step model of photoemission that accounts for all relevant aspects like matrix elements and final state effects, in a state-of-the art way. [Min11b, Min11, Min13].
Bibliography:
[Ber06] Bernevig, B. A. et al., Science 314, 1757 (2006)
[Has10] Hasan M.Z. et al., Rev. Mod. Phys. 82, 3045 (2010)
[Hir06] Hirahara T. et al., Phys. Rev. Lett. 97, 146803 (2006)
[Hof06] Hofmann P., Prog. Surf. Sci 81, 191 (2006)
[Kan05] Kane, C. L. et al., Phys. Rev. Lett. 95, 226801 (2005)
[Liu11] Liu Z. et al., Phys. Rev. Lett. 107, 136805 (2011)
[Min11] Minár J. et al., J. Electron. Spectr. Relat. Phenom. 184, 91 (2011)
[Min11b] Minár J., J. Phys.: Cond. Mat. 23, 253201 (2011)
[Min13] Minár J. et al., J. Electron. Spectr. Relat. Phen. 190, B, 159 (2013)
[Qi11] Qi X.-L. et al., Rev. Mod. Phys. 83, (2011) 1057
[Par11] Park S. R. et al., Phys. Rev. Lett. 107, 156803 (2011)
[Rau12] Rault J. E. et al., Phys. Rev. Lett. 109, 267601 (2012)
[San13] Di Sante D., et al., Adv. Mater., 25, 509 (2013)
[Ste10] Steinberg H., et al., Nano Lett., 10, 5032 (2010)
•  Électronique et optique du futur › Nanomagnétisme et oxydes : spintronique, matériaux multiferroïques et nouveaux capteurs magnétiques
Électronique et optique du futur › Nanomagnétisme et oxydes : spintronique, matériaux multiferroïques et nouveaux capteurs magnétiques  Les archives de l'IRAMIS et du DRECAM / Archives of DRECAM and IRAMIS › Matériaux, surfaces et nanostructures
Les archives de l'IRAMIS et du DRECAM / Archives of DRECAM and IRAMIS › Matériaux, surfaces et nanostructures
•  Institut Rayonnement Matière de Saclay • IRAMIS: Saclay Institute of Matter and Radiation • Laboratory of Physics and Chemistry of Surfaces and Interfaces • Service de Physique et Chimie des Surfaces et des Interfaces
Institut Rayonnement Matière de Saclay • IRAMIS: Saclay Institute of Matter and Radiation • Laboratory of Physics and Chemistry of Surfaces and Interfaces • Service de Physique et Chimie des Surfaces et des Interfaces
• Laboratory of Nanostructures Studies and Surface Imagery (LENSIS) • Laboratoire d'Etude des NanoStructures et Imagerie de Surface (LENSIS)