
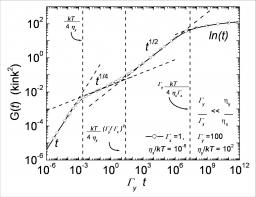
Fig.1: (--) G(t) for a rough anisotropic surface (  ). Parameters are chosen to get well-separated regimes. The various dashed and dotted lines indicates the t, t1/4, t1/2 and ln(t) regimes
). Parameters are chosen to get well-separated regimes. The various dashed and dotted lines indicates the t, t1/4, t1/2 and ln(t) regimes
Time-space fluctuations of 2-d systems may fall in various university classes depending on their symmetry and conservation laws. For metallic surfaces, at temperatures T well below the melting point, matter conservation applies for surface diffusion and thermal noise. Isotropic (dense faces) as well as highly anisotropic (vicinal surfaces) systems can be considered. h(x, y) being the surface height and  a conservative noise term, we write the 2-d Langevin equation:
a conservative noise term, we write the 2-d Langevin equation:  , with the surface Hamitonian
, with the surface Hamitonian  ,
,
where  is the anisotropic Laplacian
is the anisotropic Laplacian  ,
,  the rate constants for diffusion (related to elementary activation energies for diffusion) and
the rate constants for diffusion (related to elementary activation energies for diffusion) and  (ηx, ηy) the surface tensions (related to the kink energy and step-step interaction constant, Calogero-Sutherland model). V(h) is a localization potential favoring integral value of the surface heights for temperatures T below the roughening temperature TR.
(ηx, ηy) the surface tensions (related to the kink energy and step-step interaction constant, Calogero-Sutherland model). V(h) is a localization potential favoring integral value of the surface heights for temperatures T below the roughening temperature TR.
The Langevin equation so-defined belongs to the university class for conserved dynamics and conserved noise. Simple scaling arguments give for  ,
,  and
and  , with: α=0, β=0 and z=4 (in the present context, 0 exponent means saturation (T<TR) or logarithmic divergence). It is found (Fig.1) that for anisotropic surfaces (like vicinals) extended intermediate
, with: α=0, β=0 and z=4 (in the present context, 0 exponent means saturation (T<TR) or logarithmic divergence). It is found (Fig.1) that for anisotropic surfaces (like vicinals) extended intermediate  , and t1/2 regimes becomes possible between the initial linear variation (no correlation) and the long time logarithmic one, in agreement with experimental observations. Extensions of the various regimes (Fig.2) together with approximate analytical solutions within each of them are given.
, and t1/2 regimes becomes possible between the initial linear variation (no correlation) and the long time logarithmic one, in agreement with experimental observations. Extensions of the various regimes (Fig.2) together with approximate analytical solutions within each of them are given.
These results allowed the interpretation of measured space-time correlation functions of surface heights at thermal equilibrium. Measurements of surface tensions and diffusion rate constants follow and thus of atomic parameters.
REFERENCE: L. Barbier, E. Le Goff and B. Salanon, Surface Science 531(3) (2003) 337 and reference therein.
•  Systèmes complexes et transition énergétique › Statistical physics in mechanics
Systèmes complexes et transition énergétique › Statistical physics in mechanics
• Service de Physique et Chimie des Surfaces et des Interfaces
• Laboratory of Nano-Objects and Complex Systems (LNOSC) • GMT-MSIN : Modélisation des Surfaces Interfaces et Nanostructures
