La recherche de nouveaux états de la matière, allant au-delà de la description classique « à la Landau » suscite un très fort engouement en physique. Dans cette perspective, les travaux théoriques orientent ces recherches vers les systèmes présentant des « ordres topologiques », tels que certains « liquides de spin quantiques » et autres états fortement corrélés, caractérisés en particulier par l’absence de symétrie brisée.
Sur le plan expérimental, c’est la recherche d’une contrepartie quantique des « glaces de spins » qui a retenu l’attention. Ces composés forment un analogue magnétique de la glace d’eau, où le comportement des spins reflète exactement celui du désordre des protons dans H2O.
Une équipe internationale formée de chercheurs du PSI (Suisse), du Stanford Institute for Materials and Energy Science (USA), de l’Institut Néel à Grenoble et du LLB à Saclay a mis en évidence par diverses techniques, dont la diffusion des neutrons, un exemple de cette contrepartie quantique des glaces de spin. Plus précisément, il s’agit d’un état « glacé » particulier, où la distribution octupolaire de la densité électronique joue le rôle des moments magnétiques dans les glaces de spins classiques. L’étude des interactions montre que l’état fondamental est constitué d’une superposition quantique d’états intriqués, confirmant ainsi les prédictions théoriques sur les liquides de spins quantiques.
Il est bien admis aujourd’hui que les transitions de phase entre deux états de la matière sont bien décrites par le phénomène de brisure de symétrie. Par exemple, les états solide et liquide d’un même corps ne diffèrent que par le fait que la phase solide brise la symétrie de translation continue du liquide ; ce serait la symétrie de rotation dans le cas d’un corps ferromagnétique. Ce phénomène, rendu populaire par la théorie du physicien russe Lev Landau, dépasse de loin le cadre de la matière condensée et traverse tous les domaines de la physique moderne.
Il existe toutefois des cas qui échappent à cette description. Le système ne présente alors pas de brisure de symétrie, mais peut être néanmoins décrit à l’échelle locale par un « principe d’organisation ». Dans le cadre de la physique classique, l’état fondamental se compose alors d’une infinité (macroscopique) d’états qui adoptent cette organisation locale, tandis que dans le cas quantique, l’état fondamental est un « liquide quantique », décrit par une superposition intriquée de ces états. Ces « ordres » particuliers sont qualifiés de « topologiques » [1].
Dans le domaine du magnétisme, les composés de type « glace de spins » sont un « précurseur » bien connu de cette physique. Les moments magnétiques sont disposés au sein d’une structure cristalline cubique aux sommets de tétraèdres connectés par leurs sommets pour former un réseau pyrochlore. L’anisotropie extrêmement forte, combinée aux interactions ferromagnétiques, sont telles que chaque tétraèdre comporte nécessairement deux spins entrants et deux spins sortants (voir la figure ci-dessous). Cette « organisation locale » est tout à fait analogue à celle qui régit le désordre aléatoire des protons autour de leur atome d’oxygène dans la glace d’eau (voir figure), compte tenu de la « liaison H », d’où le nom de glace de spins ou en anglais « spin-ice ». Les glaces de spins restent ainsi désordonnées jusqu’à température nulle, sans brisure de symétrie, et présentent une entropie résiduelle identique à celle observée dans la glace d’eau. Toutefois, elles sont décrites par la mécanique classique: il n’y a pas d’interaction susceptible de faire « résonner » les configurations spin-ice entre elles pour conduire à une superposition quantique [2].
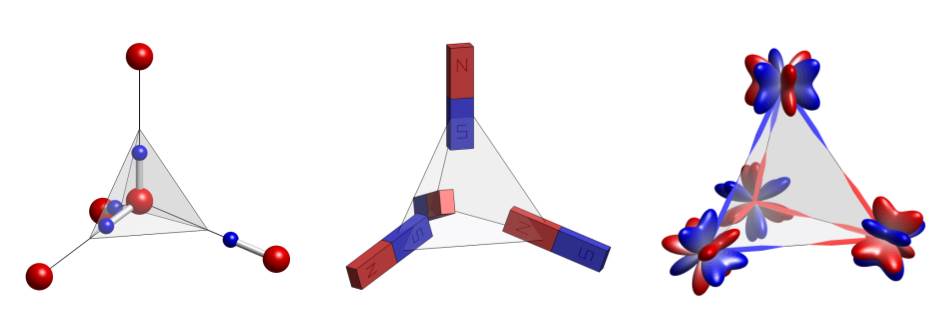
États « glacés » de la matière. Dans la glace d’eau (à gauche), les quatre atomes d’hydrogène (en bleu) autour de chaque atome d’oxygène (en rouge) sont disposés de manière aléatoire, mais toujours tels que deux d’entre eux sont proches et deux sont éloignés. Dans la glace de spins (au centre), les moments magnétiques dipolaires de matériaux choisis de manière appropriée obéissent à la même règle « 2-in-2-out ». Dans la glace octupolaire découverte par Sibille et al. [4], les sommets du tétraèdre sont occupés par des octupoles magnétiques (à droite). Leurs degrés de liberté magnétiques, représentés ici par la distribution de charge magnétique correspondante, sont contraints par une règle de glace analogue (les deux directions d’aimantation différentes sont mises en évidence par les flèches de couleur rouge et bleue le long des bords). (Images © Nicolas Gauthier)
Dans ce contexte, notre équipe rapporte des résultats qui généralisent justement ce concept au cas quantique [3]. Nous présentons le premier état de glace magnétique formé non pas par des spins mais par des degrés de liberté de rang supérieur – des octupoles. De plus, nous montrons que cet état de glace octupolaire forme un exemple de liquide quantique recherché.
L’étude porte sur un oxyde d’étain et de cérium, Ce2Sn2O7, où les ions magnétiques (ici le cérium) forment un réseau pyrochlore [4]. Des mesures d’aimantation et de relaxation de spin du muon avaient déjà montré que ce système était potentiellement un liquide de spins quantique [3], mais le travail paru dans Nature Physics explique de manière approfondie son origine microscopique.
Grâce à la diffusion des neutrons, l’équipe a pu montrer que la fonction d’onde de l’état fondamental de Ce2Sn2O7 possède des contributions qui proviennent à la fois des moments magnétiques dipolaires (les spins) mais aussi des courants formés par la distribution octupolaire de la densité électronique. Les mesures de diffusion diffuse des neutrons permettent de clairement distinguer ces deux contributions. Par le calcul, il a alors pu être déduit que l’interaction dominante est le couplage entre octupoles. Cependant, des interactions spin-spin existent aussi. Quoique plus faibles, elles jouent un rôle important car elles permettent de faire résonner les configurations de type « glace » entre elles. Au lieu de stabiliser un état classique, comme dans les glaces de spins traditionnelles, le couplage spin-spin a donc un rôle central pour stabiliser un état fondamental constitué d’une superposition quantique de ces états de glace.
Les mesures de diffusion inélastique des neutrons ont également permis de révéler un spectre d’excitations très original. Dans les composés magnétiques usuels, les excitations peuvent être vues comme des bosons portant un spin entier. Dans ce cas, les neutrons révèlent la dispersion de ces bosons, dans l’espace des phases formé par le moment Q et l’énergie E, sous la forme d’une relation bien définie liant Q et E. Dans le cas de Ce2Sn2O7, un neutron qui interagit avec l’échantillon modifie localement la distribution de courants et crée un défaut dans la glace. Ce défaut peut se séparer en deux sous-entités, portant des nombres quantiques fractionnaires, et capables de se déplacer dans le réseau. Les neutrons révèlent alors un spectre caractéristique de la distribution de ces sous-entités et qui se présente sous la forme d’un « continuum » dans l’espace (Q,E).
Les phases de la matière qui sont principalement stabilisées par des interactions multipolaires sont rares. La glace octupolaire est unique parmi celles-ci et nos résultats expérimentaux sont cohérents avec la prédiction récente d’un liquide de spins quantique en trois dimensions [5]. Des interactions multipolaires plus élevées sont connues ou supposées être l’une des clés pour comprendre un plus large éventail d’ordres « cachés » dans différents systèmes de la physique de la matière condensée, par exemple des matériaux à fermions lourds ou les supraconducteurs à haute température critique. Réunir ce domaine de recherche avec le monde fascinant de la physique « des glaces » et des liquides de spins quantiques en général, promet d’ouvrir de nouvelles perspectives – et peut-être des applications inattendues dans le domaine des technologies quantiques.
Références :
[1] X.-G. Wen, Quantum Field Theory of Many-Body Systems, Oxford University Press, Oxford, 2004.
[2] “Quantum spin liquids: a review”,
Savary, L & Balents, L. Rep. Prog. Phys. 80, 016502 (2016)

[3] « A quantum liquid of magnetic octupoles on the pyrochlore lattice »,
Sibille R, Gauthier N, Lhotel E, Porée V, Pomjakushin V, Ewings RA, Perring TG, Ollivier J, Wildes A, Ritter C, Hansen TC, Keen DA, Nilsen GJ, Keller L, Petit S, Fennell T, Nature Physics (2020). (Free-to-view version)
[4] « Candidate quantum spin liquid in the Ce3+ pyrochlore Stannate Ce2Sn2O7 »,
Sibille R, Lhotel E, Pomjakushin V, Baines C, Fennell T and Kenzelmann M, Phys. Rev. Lett. 115, 097202 (2015).
[5] “Symmetry enriched U(1) topological orders for dipole-octupole doublets on a pyrochlore lattice”, Li, Y.-D. & Chen, G. Phys. Rev. B 95, 041106 (2017).
Contact CEA-IRAMIS : S. Petit, LLB/NFMQ UMR 12 CEA-CNRS, Université́ Paris-Saclay, CEA Saclay, Gif-sur-Yvette
Collaboration :
- R. Sibille, V. Porée, V. Pomjakushin, L. Keller & T. Fennell : Laboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, Villigen, Switzerland
- N. Gauthier : Stanford Institute for Materials and Energy Science, SLAC National Accelerator Laboratory and Stanford University, Menlo Park, CA, USA
- E. Lhotel : Institut Néel CNRS, Université Grenoble Alpes, Grenoble, France
- R. A. Ewings, T. G. Perring, D. A. Keen & G. J. Nilsen : ISIS Pulsed Neutron and Muon Source, STFC Rutherford Appleton Laboratory, Harwell Campus, Didcot, UK
- J. Ollivier, A. Wildes, C. Ritter & T. C. Hansen : Institut Laue-Langevin, Grenoble, France