
Guillaume MOUROT , Elisabeth BOUCHAUD
Coll: Stéphane MOREL, Gérard VALENTIN (Laboratoire LRBB, Université de Bordeaux, France)
Four points bending specimens of high strength Portland cement (maximum grain size of the sand is 2 mm) of six different sizes ranging over a decade (height D of the samples varies from 20 to 200 mm) were broken, and the fracture surfaces were recorded with an optical profiler along regular grids (mesh size 20 to 60 mm). The description of their morphology requires two roughness exponents: One of them – so-called “local” in the present context – is the universal exponent ζ≈0.8; the other one, ζg, called “global”, actually describes the evolution of the amplitude of roughness (see Fig. 2) when the distance from the initial notch is increased. Correlatively, the upper bound of the scaling domain, ξ, also evolves with the distance to the notch, and reaches a maximum value ξsat at a distance ysat. Figure 3 clearly shows that ξsat is proportional to D. It is clear that the origin of size effects resides in the growth of the FPZ, the trace of which can be “read” in terms of anomalous scaling on the fracture surfaces.
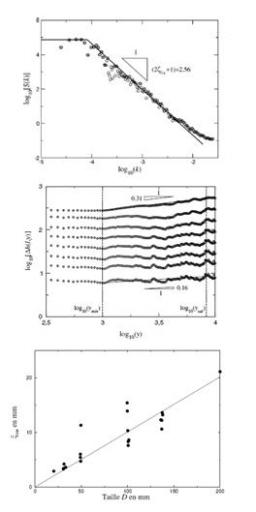
Top: Log-log plot of the power spectrum S(k) of a profile perpendicular to the direction of crack propagation. The power law involves an exponent 2ζ+1, and the best fit corresponds to ζ≈0.79. Middle: Log-log plot of the RMS roughness as a function of the distance y to the initial notch. Roughening occurs for values of y between ymin and ymax. ξsat as a function of the sample size D; ξsat ≈ 9D/100.
•  Systèmes complexes et transition énergétique › Statistical physics in mechanics
Systèmes complexes et transition énergétique › Statistical physics in mechanics
• Laboratory of Physics and Chemistry of Surfaces and Interfaces • Service de Physique et Chimie des Surfaces et des Interfaces
• Laboratory of Nano-Objects and Complex Systems (LNOSC) • GMT-MSIN : Modélisation des Surfaces Interfaces et Nanostructures









