For direct access to the movie of the iterative retrieval (gif format), click here
FROG CRAB is a method for the complete temporal characterization of attosecond XUV fields. It consists in generating an electron wave-packet in the continuum by photoionizing atoms with the attosecond field, and in using a low-frequency dressing laser pulse as a phase gate for FROG-like measurements on this wave-packet. This method is valid for XUV fields of arbitrary temporal structure, e.g. complex isolated attosecond pulses, or trains of non-identical attosecond bursts, such as those that are generated through high-order harmonic generation in gases. It establishes a direct connection between the main attosecond characterization techniques demonstrated experimentally so far [1,2] and considerably extends their scope, thus providing a general perspective on attosecond metrology. This method is described in details in [3,4].
The goal of this web page is to show the iterative retrieval of both the attosecond field and the laser-induced phase gate from a simulated CRAB trace for a non-trivial attosecond field, consisting of a central main pulse surrounded by satellites pulses. CRAB is the only existing method for the full characterization of such complex atto fields. The CRAB trace used here is the same as the one as in figure 3 of [3].
The retrieval is achieved with a home-made version of an iterative algorithm that is commonly applied on FROG measurements of visible pulses : Principal Component Generalized Projections Algorithm (PCGPA) [5]. It is simple, very efficient, and is easy to program using Labview and its VI library. PCGPA is especially well suited to blind FROG measurements, i.e. when the pulse and the gate are independent functions, as is the case in CRAB.
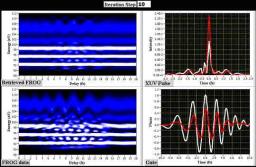
The movie showing the convergence of the algorithm can be downloaded here. It presents four panels, as on the picture below.
This case corresponds to the CRAB trace of a complex atto field, gated by an 800 nm chirped laser pulse of 7 fs duration and 0.05 TW/cm2 intensity . The exact CRAB trace (lower left panel) has been calculated using the strong-field model [3,4]. The spectrum of this atto field consists of discrete peaks spaced by about 3 eV in its lower part, and a continuous component in its upper part. This qualitatively corresponds to what would be obtained by selecting the end of the plateau and the cut-off of the high-harmonic spectrum generated in a gas by a few-cycle laser pulse.
Initial guess:
The algorithm needs an initial guess for the attosecond field and the laser-induced gate. For the attosecond field, the initial guess can be the Fourier transform of the XUV spectrum, assuming a flat spectral phase. The initial guess we use for the laser-induced gate is as simple as it can be : it is a constant function equals to 1 (i.e. we initially assume that there is no gate).
Iterative retrieval:
Despite the complexity of the attosecond field, after 300 iterations of PCGPA, the retrieved CRAB trace (upper left panel) converges to the exact one, and the retrieved atto field and laser electric field (red curves in right panels) perfectly match the exact fields (used to calculate the exact CRAB trace, white curves in right panel)). In these iterative calculations, the amplitude of the laser-induced gate is imposed and fixed to 1. Note that PCGPA first starts by retrieving the laser-induced gate phase, and then refines the attosecond field to get a better match between the retrieved CRAB trace and the exact one. The CRAB trace consists of a 256x256 square matrix. This retrieval takes about 10 minutes on a standard personal computer.
[1] R.Kienberger et al., Nature 427, p.817 (2004)
[2] P.M. Paul et al., Science 292 (2001) 1689
[3]Y.Mairesse and F. Quéré, Frequency-Resolved Optical Gating for Complete Reconstruction of Attosecond Bursts,
Phys. Rev. A, 71 (2005) 0011401(R).
[4] F. Quéré, Y.Mairesse and J.Itatani, Temporal characterization of attosecond xuv fields, Journal of Modern Optics, 52, 339-360 (2005)


 Interaction laser-matière
Interaction laser-matière Interaction laser-matière en champ fort
Interaction laser-matière en champ fort