Ce qui distingue les faisceaux laser de la lumière ordinaire est leur grande cohérence spatiale. Cette caractéristique a des impacts majeurs sur de multiples méthodes de mesure, en physique atomique fondamentale, métrologie ou microscopie. Cependant, les sources laser pulsées utilisées peuvent présenter des fluctuations tir à tir importantes, qui entraînent erreurs statistiques et pertes d’information. Un moyen de s'affranchir du problème est de pouvoir mesurer la cohérence individuelle de chaque impulsion lumineuse, ce qui jusqu’à présent n’était pas accessible.
Le CEA/LIDYL, en collaboration avec l’IST de Lisbonne, a mis au point une nouvelle technique de mesure de la cohérence spatiale, basée sur l’utilisation d’un réseau non redondant d’ouvertures nanométriques [1]. Cette technique est robuste vis-à-vis des fluctuations de pointé et d’intensité du faisceau. Appliquée en parallèle avec les expériences, elle permettra de connaître la cohérence spatiale réelle à l'instant de la mesure et d'améliorer ainsi sa précision.
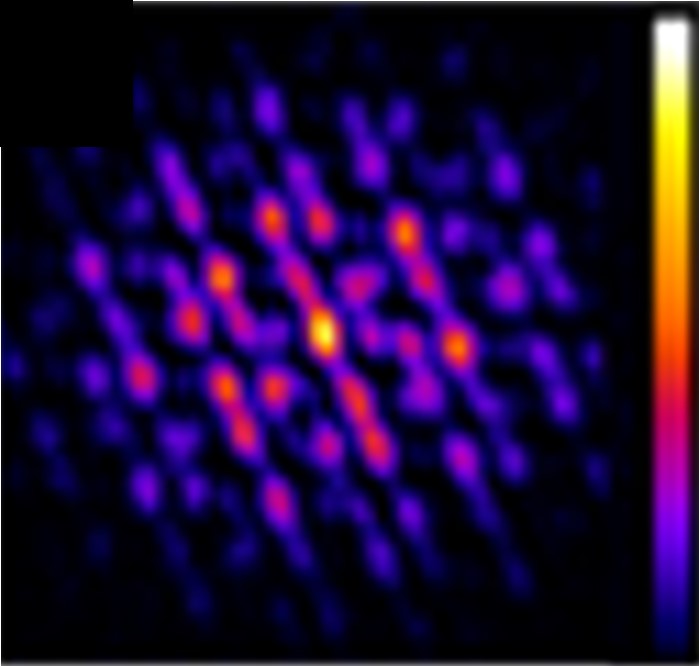
La cohérence spatiale est une propriété d’un faisceau lumineux qui caractérise la relation de phase à une longueur d'onde donnée, entre deux points de sa section transverse plus ou moins distants l’un de l’autre. Les sources traditionnelles, telles que les ampoules à filament ou les diodes électroluminescentes, ont un degré de cohérence spatiale quasi nul, alors qu'il est proche de un, sa valeur maximale, pour les faisceaux lasers. Concrètement, une bonne cohérence autorise la possibilité de générer des interférences bien contrastées entre différentes parties du faisceau, ce qui est utilisée par exemple dans la microscopie holographique ou en métrologie. La mesure de cohérence peut de plus permettre d’améliorer la précision d’analyse de données expérimentales. Ainsi, en imagerie par diffraction cohérente, technique de microscopie qui remplace l’utilisation des objectifs traditionnels introduisant des aberrations par des algorithmes, la prise en compte du degré réel de cohérence par ces algorithmes améliore la résolution des images [2].
Les nouvelles sources de rayonnement de courtes longueurs d’onde (de 100 à 5 nm) que sont les impulsions harmoniques laser d’ordre élevé ou les lasers à électrons libres possèdent elles aussi un très fort degré de cohérence spatiale. De par leurs propriétés spatiales et temporelles, ces sources révolutionnent de nombreux domaines de la science, de la physique atomique et moléculaire à la cristallographie, de la connaissance des plasmas à la microscopie. Cependant, leurs propriétés présentent d’importantes fluctuations d'une impulsion à une autre, notamment leur degré de cohérence spatiale. Différentes techniques de mesure de cette quantité sont actuellement utilisées, la principale étant basée sur le principe de la célèbre expérience des fentes d’Young. Toutes ces techniques nécessitent cependant soit la mesure simultanée du profil d’intensité du faisceau et des figures d’interférences, soit un ensemble de caractérisations spatiales séquentielles, ce qui ne permet pas la prise en compte en temps réel des caractéristiques du faisceau.
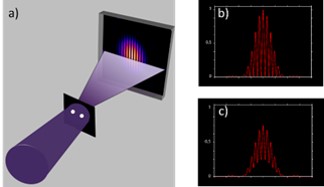
Afin de coupler ces mesures et de les réaliser sur un unique tir laser, le CEA/LIDYL a alors mis au point une méthode de mesure de cohérence spatiale transverse à l'aide d'un interférogramme spécifique basé sur l’utilisation d’un réseau bidimensionnel « non redondant » de trous d’Young. Ce type de réseau permet de réaliser simultanément la mesure d’Young pour chaque distance entre les différents points sélectionnés au sein de la section transverse du faisceau. Il permet donc de mesurer la cohérence spatiale selon différentes directions et d’obtenir ainsi une cartographie 2D d'une impulsion unique. De plus, l’utilisation d’un trou de référence commun à tous les couples de points considérés (trou #1 dans la figure 3) permet à la méthode d’être insensible aux fluctuations d’intensité et de pointé du laser.
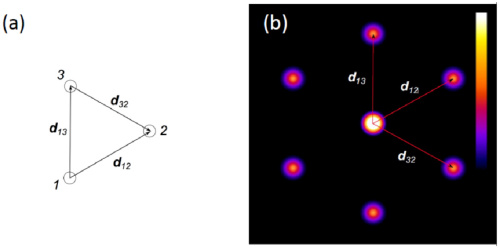
Cette approche a été démontrée expérimentalement avec un faisceau de longueur d’onde λ = 32 nm, issu de la génération d’harmoniques laser d’ordre élevé dans un gaz. Une analyse statistique a montré qu’une prise de données sur un temps long, c’est-à-dire accumulant sur plusieurs impulsions laser, résultait en une diminution du degré de cohérence apparent du faisceau lumineux. Pouvoir caractériser la stabilité tir à tir de la source permet d'exploiter au mieux sa véritable cohérence spatiale transverse et ceci même pour une impulsion unique !
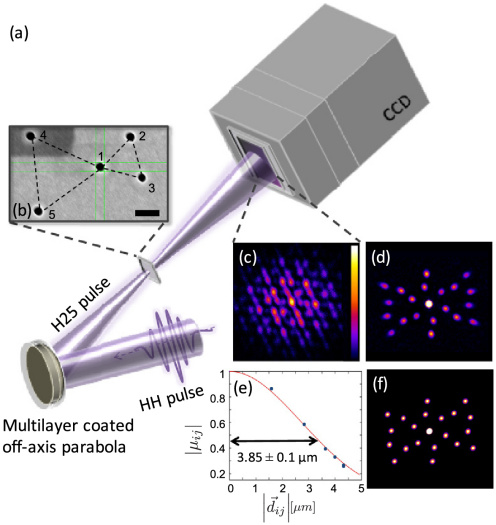
Cette technique, par sa simplicité, est compatible avec un très large panel de sources de lumière, qu’elles soient monochromatiques (laser plasma, synchrotron) ou ultra-brèves, (lasers à électrons libres, impulsions attosecondes). Cette dernière catégorie requiert néanmoins un traitement numérique supplémentaire afin de prendre en compte leur très grande largeur spectrale [3].
En perspective, la prise en compte de la méthode dans les algorithmes de reconstruction d’image en microscopie par holographie est actuellement à l’étude. La connaissance en temps réel du degré de cohérence spatiale d'impulsions de lumière laser a aussi bien d'autres implications sur de nombreuses méthodes de mesure, implantées autour des serveurs laser, des synchrotrons ou des lasers à électrons libres, qui couvrent de nombreux domaines.
Références :
Références :
[1] « Single-shot spatial coherence characterization of x-ray ultrafast sources”
J. Duarte, A. I. Gonzalez, R. Cassin, R. Nicolas, M. Kholodstova, W. Boutu, M. Fajardo and H. Merdji, Optics Letters 46, 1764-1767 (2021)
[2] « Reconstructing state mixtures from diffraction measurements »
P. Thibault, A. Menzel, Nature 494, 68-71 (2013).
[3] « Broadband coherent diffractive imaging »
J. Huijts, S. Fernandez, D. Gauthier, M. Kholodtsova, A. Maghraoui; K. Medjoubi, A. Somogyi, W. Boutu and H. Merdji, Nature Photonics 14, 618 (2021).
________________________________________
Contact CEA-IRAMIS : Willem Boutu (LIDYL/ATTO)
Collaboration :
- M. Fajardo, Instituto de Plasmas e Fusão Nuclear, IST Lisboa, Portugal.



