Thomas Blenskia et Bogdan Cichockib
aCEA Saclay, DSM/IRAMIS/LIDYL, Bât 522, F91191 Gif-sur-Yvette Cedex, France
bInstitute of Theoretical Physics, Warsaw University, Hoza 69,
00-681 Warsaw, Poland
Dans un plasma dense et chaud (étoiles, interaction avec un laser nanoseconde, fusion inertielle …), les atomes sont partiellement ionisés et forment un mélange d'ions et d'électrons à la dynamique très complexe. Une bonne modélisation de cet état doit être fondée sur une compréhension du système étudié permettant de reproduire l'ensemble de ses propriétés, pour finalement révéler ses particularités Pour un plasma, le bilan radiatif et les propriétés optiques sont des paramètres macroscopiques particulièrement importants à connaître, mais cela nécessite de disposer d'un modèle quantique prenant bien en compte l'ensemble des états atomiques excités tout en restant thermodynamiquement cohérent. C'est ce type de modèle que les théoriciens tentent de développer activement depuis plus de cinquante ans. La difficulté de construire un modèle quantique et thermodynamique d'un plasma a été récemment surmontée par les travaux [6,7] entrepris au DRECAM/SPAM en collaboration avec B. Cichocki de l’Université de Varsovie.
Nous nous sommes intéressés aux plasmas denses et chauds (densité 1019 à 1025 e-/cm3, température électronique 104 à 106 K) que l'on rencontre par exemple en astrophysique ou en laboratoire, où ils peuvent être produits par irradiation de la matière avec un laser de haute énergie. Dans un plasma composé d’éléments de nombre atomique Z moyen ou élevé, les atomes ne sont que partiellement ionisés même à des températures très élevées. Les électrons liés jouent alors un rôle dominant dans l’absorption et l’émission de photons par le plasma. Par exemple, dans la partie interne du Soleil, la présence de faibles traces des ions du fer (Z=26) et d’autres métaux, qui gardent une population d’électrons liés, détermine fortement le transfert d’énergie radiative.
Parmi les premiers modèles atomiques d'un plasma, on peut citer ceux fondés sur l'approche de Feynman, Metropolis et Teller (FMT, 1947) [1], où les états électroniques suivent une distribution de Thomas-Fermi (quasi-classique) et où l'énergie est distribuée selon une distribution de Fermi-Dirac. L'absence de couches électroniques dans ce type de modèle limite fortement leur application puisqu'elle le rend inadapté à l'étude des propriétés optiques. Cependant le modèle FMT possède le grand avantage d'assurer une bonne description thermodynamique (car fondé sur une approche variationnelle) et fournit une équation d’état simple reliant le nombre atomique Z, la densité ionique et la température (ceci permettant d'en déduire par exemple la pression). Cette information est réutilisée, par exemple, dans des simulations hydrodynamiques globales d'une expérience.
Dans le cas d'un plasma fortement couplé, dans lequel le rapport des énergies potentielle et cinétique des ions est au moins de l'ordre de l'unité, l’écrantage électronique assure, en moyenne, la quasi-neutralité de la région au voisinage de chaque ion. Cette région peut alors être modélisée comme une cellule ionique neutre (sphère de Wigner-Seitz de rayon R). L'approche FMT variationnelle consiste à minimiser l'énergie libre électronique en tenant compte de cette contrainte sur la densité électronique.
Le modèle FMT a été étendu à des théories quantiques comme le modèle de l’atome moyen [2], où les électrons liés à l’intérieur de la cellule ionique sont représentés par des états quantiques et où les électrons libres restent décrits par un fluide (Thomas-Fermi). Signalons aussi des modèles auto-cohérents plus ambitieux [3–5], où les deux populations d’électrons, liés et libres, sont traitées de manière quantique. Cependant toutes ces extensions ne conservent pas le caractère variationnel du modèle FMT et ne surmontent donc pas d'importantes difficultés, en particulier en ce qui concerne la pression.
La difficulté de construire un modèle quantique et thermodynamiquement acceptable d'un plasma a été surmontée par les travaux [6,7] entrepris au DRECAM/SPAM en collaboration avec B. Cichocki de l’Université de Varsovie. Initialement, le milieu est décrit par des densités électroniques et ionique uniformes. Ensuite, on ajoute un ion ayant une configuration électronique d’électrons liés et libres qui est plongé dans le champ moyen auto-cohérent (voir figure) avec la prise en compte approximative des autres ions et leurs électrons. Cette approximation est suffisante tant que la dimension caractéristique d'écrantage reste inférieure à la valeur de R. La méthode est répétée pour l'ensemble des configurations électroniques accessibles aux ions (dans des états fondamental et excités) sur lequel on fait une moyenne thermodynamique. La prise en compte effective de façon quantique de l'ensemble des configurations électroniques excitées, ainsi que des électrons délocalisés, rend cette approche bien plus riche que le modèle FMT initial, tout en conservant son aspect thermodynamique et en reproduisant correctement les principaux paramètres.
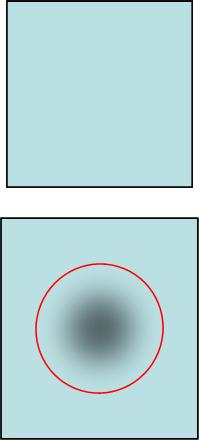
Cette méthode assure donc la cohérence thermodynamique de la modélisation tout en permettant une description des propriétés radiatives des plasmas chauds et denses. Ainsi les spectres expérimentaux dont une des caractéristiques est de présenter des raies spectroscopiques très élargies peuvent être mieux interprétés. Il devient alors possible de déduire la température électronique et ionique et la pression du plasma. Enfin, une version relativiste, incluant entre autres le couplage spin-orbite, est en cours de développement.
[1] R. P. Feynman, N, Metropolis, E. Teller, Phys. Rev. 75 (1949) 1561.
[2] B.F. Rozsnyai, Phys. Rev. A, 5(3) (1972) 1137.
[3] D. A. Liberman, Phys. Rev. B 20 (1979):4981.
[4] F. Perrot, code AJCI (“Atome dans le Jellium de Charge Imposée”), rapport interne CEA, résultat non publié.
[5] B. Wilson, V. Sonnad, P. Sterne and W. Issacs, JQSRT 99 (2006) 658.
[6] T. Blenski, B. Cichocki, « Variational theory of average-atom and superconfigurations in quantum plasmas », Physical Review E 75, (2007) 056402.
[7] T. Blenski and B. Cichocki, « Variational approach to the average-atom-in-jellium and superconfigurations-in-jellium models with all electrons treated quantum mechanically », High Energy Density Physics 3 (2007) 34.