Major Results
Quasi-linear model of turbulence We have developed a new quasi-linear model of turbulence in collaboration with J.-P. Laval (Lille University) and S. Nazarenko (Warwick, GB). We have shown that this model allows simple understanding of the small scale intermittency. With J. Mc Williams (UCLA), we have also shown how this model could lead to a stochastic approach of the closure problem of Navier-Stokes equations. This method has been applied to the computation of 2D and 3D energy spectra in fluid turbulence with O. Zagorosvski (Warwick, GB), and to the computation of torques in von Karman experiment. The quasi-linear model of turbulence has also been applied to convection. The scaling laws of the turbulent transport have been derived. Logarithmic corrections to scaling have been obtained. This approach has been generalized to the case of large Prandtl number convection, leading to an explanation for an experimental controversy between several experiments.
Astrophysical flows Turbulence is an important issue in modeling astrophysical objects. In stellar interiors, turbulent mixing modifies the chemical composition and therefore has a strong impact on the evolution of the star, whereas in disks, the accretion of matter onto the central object is possible only through turbulent dissipation. These objects are characterized by their non-uniform rotation; and one knows since the early development of stability theories that such flows are prone to hydrodynamical instabilities, which may lead to turbulence. However, according to linear perturbation theory, the non uniform rotation observed in stars and in disks should be linearly stable. Therefore, in these two instances, any shear-induced hydrodynamic instability is necessarily non-linear i.e. induced by a finite amplitude disturbance. The Couette-Taylor flow - a fluid layer sheared between two coaxial cylinders rotating at different speed - is an excellent candidate to mimic astrophysical flows : depending on the rotation speed of each cylinder, one can obtain various flow regimes with increasing or decreasing angular velocity and/or angular momentum. In collaboration with J. P. Zahn (Meudon Observatory), we have set up a new Couette-Taylor experiment, in order to extend the search of differentially rotating flows which are unstable to finite amplitude perturbations, and to study the properties of the turbulence arising then. We have verified that turbulence may occur in linearly stable regime and we have studied the influence of rotation on the sustained turbulence thresholds. Also, it was possible for the first time to measure velocity fluctuations in such configurations and to investigate some transport properties and their dependance on rotation. Further work consists in reformulating our results in the more general context of rotating shear flows via a unique formalism which would extend from Taylor-Couette flow to rotating plane Couette flow. From the theoretical side, the influence of stratification has been studied in collaboratio with avec C. Normand (SPhT), F. Hersant and J-P Zahn. A new criterion for instability has been proposed, and confirmed via a numerical exploration. Next, a new model of torques scaling in Taylor-Couette experiment has been developed. This theory has been applied to circumstellar disks, and used to prove that they are indeed turbulent.
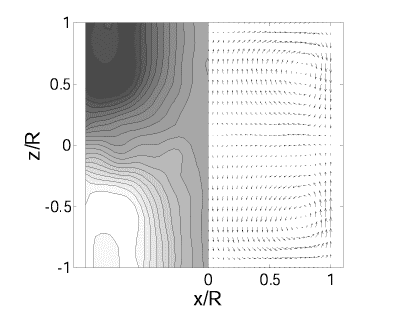
Mean velocity field; the left side (resp. right side) of the figure represents the azimutal (resp. poloidal) flow; the propellers are situated at the top and bottom.
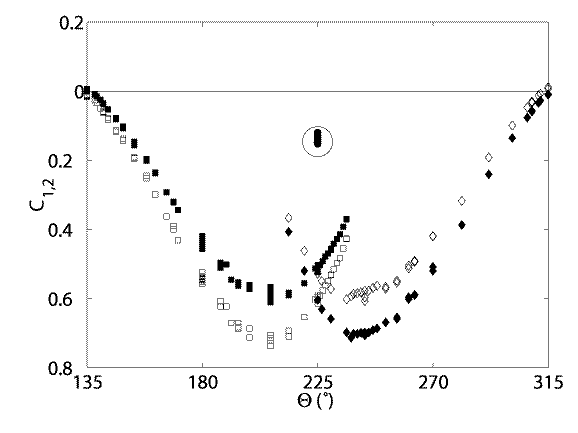
Von Karman flows Von Karman water experiment. (a) Mean velocity field the left side (resp. right side) of the figure represents the azimutal (resp. poloidal) flow; the propellers are situated at the top and bottom. (b) bifurcation diagram representing the torques C_1 and C_2 of the two motors as a function of the arctangent of the ratio of the two frequencies (225 corresponds to f_1=f_2); circles correspond to the usual flow and squares and diamonds to the bifurcated flow. The generic term von Karman flows designates the class of flows induced by the counter-rotation of two coaxial impellers located at both ends of a cylindrical vessel. These flows display differential rotation and large scale helicity and are supposed to be good candidates to the realization of an experimental homogeneous fluid dynamo. We have studied such flows in a water experiment, half-scale model of the sodium VKS experiment presented in the following. Different propellers have been used to drive the flow at rotation rates corresponding to a highly turbulent flow (Re = 5.10^5 ) and we have characterized the flow both globally (visualization, torque) and locally (pressure and velocity). Measurements of the mean velocity field have been performed by laser velocimetry techniques and reveal the existence of two counter-rotating toroidal cells combined with two recirculating poloidal cells. Note that velocity fluctuations appear to be of the order of magnitude of the mean velocity, in particular in the equatorial plane, where a strong mixing layer is observed.
Torque measurements are in agreement with the expected turbulence scaling, but when the flow is driven by propellers with curved blades rotating counter-clockwise, one observes a global bifurcation of the usual mean turbulent flow towards a flow with a unique poloidal recirculation cell. This bifurcation is strongly hysteretic and the bifurcated flow is associated with a large increase of the torque. Using a new approach based on angular momentum conservation arguments, we have obtained a simple expression for the torque applied by the forcing mechanism and been able to link the velocity fluctuations correlations to the turbulent drag. By measuring the cospectrum of the velocity fluctuations, we also present evidence that the drag torque is dominantly associated with the large scale dynamics of the flow. Finally, a new von Karman experiment including a global rotation of the apparatus has been constructed in order to study the influence of the Coriolis force on this type of flows. The first results obtained reveal a bidimensionalization of the mean flow in agreement with the Taylor-Proudman theorem (no dependence along the axis of rotation) but no decrease of the turbulent fluctuations seems to be observed
Collaborations
•  Statistical physics and complex systems › Statistical physics and complex systems
Statistical physics and complex systems › Statistical physics and complex systems
• UMR 3680 - Service de Physique de l'Etat Condensé (SPEC) • UMR 3680 - Laboratory of Condensed Matter Physics (SPEC)
• SPHYNX