





2. A brief historical review of electron hydratation
2.1 The absorption spectrum of the hydrated electron
2.2 The dielectric continuum theory
2.3 The statistical approach
| After the first experimental proof of the existence of the hydrated electron by Hart and Boag [1], a lot of experimental studies have been carried out in order to understand the influence of the pH, the temperature, the ionic character and the isotopic substitution on the absorption spectrum [2]. In particular the temperature and the H/D isotopic substitution have been carefully studied by Michael and co-workers [8] and Jou and Freeman [9]. In the latter study, the authors propose a mathematical form that takes into account the asymmetry of the absorption spectrum. They propose a Lorentzian shape for the blue part of the absorption spectrum and a Gaussian shape for the red part. |
 |
Despite the number of studies devoted to the hydrated electron mainly with pulse radiolysis experiments [2-4] little was known on the dynamics of electron hydration. In those early times the idea generally accepted was that the hydrated electron was solvated by the dielectric reaction of the media (i.e. the dielectric continuum theory). This theory was developed in the 1930’s by Landau [10] and by Fröhlich [11] in the 1940’s. An improvement of those theories was introduced by Jortner [12,13] who got a better estimation of the radius of the solvated electron. In order to take into account the short range local structure of the solvent some works have been devoted since the 1970’s to new electron solvation models [14-17]. The semi-continuum models are based on the idea that « it was not possible » to treat completely the structure of the global system (one electron and a liquid). In those models the space was divided in two distinct regions. The first one is the inside of a sphere. In this region the interactions between the electron and the water molecules of the first solvation shell are specifically taken into account. |
The second region is the rest of the space. The electron interacts with that region through a dielectric continuum model. Consequently the solvation dynamics was expected to be governed by the Debye equation [11] and characterised by a continuous shift of the absorption spectrum from the infrared to the visible with a characteristic time defined as follows:

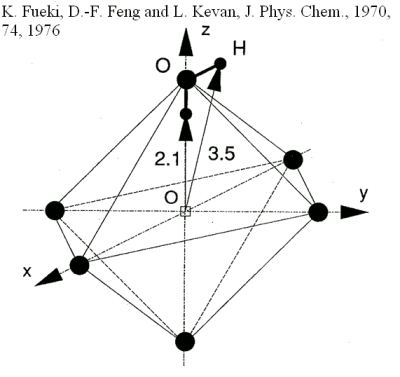
| One of the models developed is the one of Fueki, Feng and Kevan (FFK) [17]. This model is based on the interpretation of EPR experimental data [18]. The authors found that in aqueous glasses the first solvation shell was composed of six water molecules having their OH bond pointing towards the centre of the cavity [19]. This cavity model is the first that does not suppose a dipolar orientation of the first solvation shell. However the authors just took into account the dipolar interaction of the first solvation shell molecules with the electron. Using the same model for the first solvation shell but with a more sophisticated electron-water pseudopotential [20], Pommeret and Gauduel [21] computed the fundamental energy of the electron. |  |
In the late 1980’s a new approach of the electron hydration started, based on the propagation of a quantum solute in a classical bath. The first algorithms used were based on the path integral developed by Feyman [22] for the theoretical aspect and applied by Chandler and co-workers [23-26] to simple fluids. With Quantum Path Integral Monte Carlo (QPIMC) [27-29] or Molecular Dynamics (QPIMD) [30-33] it is impossible to extract any dynamical features since the time used in QPIMD calculations is not real due to the necklace of the quantum particle. However it is possible to get some structural information from those computations. Sprik and Klein have reviewed the work on electron solvation in polar fluids [34]. All computations agree on the fact that the water molecules of the first solvation shell are oriented towards the centre of the cavity.
| Using sophisticated techniques originally used for intense laser beam propagation that allow the numerical resolution of the Schrödinger equation [35], it was possible not only to determine the fundamental state for a given solvent configuration but also the excited states and the absorption spectrum of the hydrated electron [36,27] (see table above). Those studies clearly demonstrate that the excited states of the hydrated electron are not degenerated. The fundamental was already known as a s-like state and the discovered excited states were found to be p-like for the three first. According to Schnitker and co-workers [36], the non-degenerated p-like states account for the width of the hydrated electron absorption spectrum. It is worthwhile to note that despite the very good agreement between experiment and theory for the WFMBP model [28] at ambient temperature, it does not correctly simulate the temperature dependence of the absorption spectrum of the hydrated electron. |
References:
[8] B.D. Michael, E.J. Hart and K.H. Scmidt, J. Phys. Chem., 1971, 75, 2798
[9] F.-Y. Jou and G.R. Freeman, J. Phys. Chem., 1979, 83, 2383
[10] L. Landau, Phys. Z. Sowjetunion, 1933, 3, 664
[11] H. Fröhlich, Theory of Dielectrics, Oxford at the Clarendon Press, 1949
[12] J. Jortner, J. Chem. Phys., 1959, 30, 839
[13] J. Jortner, Mol. Phys., 1962, 5, 257
[14] D.A. Copeland, N.R. Kestner and J. Jortner, J. Chem. Phys., 1970, 53, 1189
[15] D.-F. Feng and L. Kevan, Chem. Rev., 1980, 80, 1
[16] M. Tachiya and A. Mozumder, J. Chem. Phys., 1974, 60, 3037 ; ibid, J. Chem. Phys., 1974, 61, 3890
[17] K. Fueki, D.-F. Feng and L. Kevan, J. Phys. Chem., 1970, 74, 1976
[18] L. Kevan, Radiat. Phys. Chem., 1981, 17, 413
[19] See Figure 4 (page 416) of reference 18
[20] J. Schnitker and P.J. Rossky, J. Chem. Phys., 1987, 86, 3462
(21] S. Pommeret and Y. Gauduel, J. Phys. Chem., 1991, 95, 4126
[22] Feynman
[23] D. Chandler and P.G. Wolynes, J. Chem. Phys., 1981, 74, 4078
[24] K.S. Schweitzer, R.M. Stratt, D. Chandler and P.G. Wolynes, J. Chem. Phys., 1981, 75, 1347
[25] D. Chandler, Y. Singh and D.M. Richardson, J. Chem. Phys., 1984, 81, 1975
[26] A.L. Nichols III, D. Chandler, Y. Singh and D.M. Richardson, J. Chem. Phys., 1984, 81, 5109
[27] A. Wallquist, G. Martina and B.J. Berne, J. Phys. Chem., 1988, 92, 1721
[28] A. Wallquist, D. Thirumalai and B.J. Berne, J. Chem. Phys., 1987, 986, 6404
[29] M. Sprik, R.W. Impey and M.L. Klein, J. Stat. Phys., 1986, 43, 967
[30] C. Romero and C.D. Jonah, J. Chem. Phys., 1989, 90, 1877
[31] C.D. Jonah, C. Romero and A. Rahman, Chem. Phys. Lett., 1986, 123, 209
[32] J. Schnitker and P.J. Rossky, J. Chem. Phys., 1987, 86, 3471
[33] P.J. Rossky and J. Schnitker, J. Phys. Chem., 1988, 92, 4277
[34] M. Sprik and M.L. Klein, Comp. Phys. Rep., 1988, 7, 147
[35] M.D. Feit, J.A. Fleck and A. Steiger, J. Comp. Phys., 1982, 47, 412
[36] J. Schnitker, K. Motakabbir, P.J. Rossky and R. Friesner, Phys. Rev. Lett., 1988, 60, 456
[37] J. Schnitker and P.J. Rossky, J. Chem. Phys., 1987, 86, 3462
| << Previous | Summary | Next >> |