
The present work is at the interface of studies of fracture and structure of materials. What can be known from a fracture surface? Can we improve our knowledge of a material structure from its fracture surfaces? Fracture surfaces of a quasicrystal are here considered.
On the quasicrystal side (QC), aperiodic materials can be seen as the projection in three dimensions of a periodic structure in a virtual space of higher dimension (6 for QC with icosahedral (i-) symmetry). In real space, the structure may be described as an aperiodic assembly of overlapping, so called Bergman or Mackay, clusters. This very cluster structure was suggested to be at the origin of the mysterious stability of QCs. Clusters being able to be preserved in a fracture experiment, analysis of fracture surfaces are an attempt to found evidence of their relevance in the structure.
On the fracture side, roughness of the fracture surface of various heterogeneous materials (Al alloy, mortar, silica glass…) was shown to be self-similar whatever the heterogeneity characteristic length is. This universal behavior with z = 0.8 power law dependence is pointed out from the elementary grain scale up to the process zone size given by  . Accordingly, i-AlPdMn QC offers unexplored conditions: the extension of the process zone (estimated from the toughness ΚIc and the upper yield stress σY at room T) is of the order of ~ 0.09 nm, lower than the atomic size, making i-AlPdMn a hyper-brittle material.
. Accordingly, i-AlPdMn QC offers unexplored conditions: the extension of the process zone (estimated from the toughness ΚIc and the upper yield stress σY at room T) is of the order of ~ 0.09 nm, lower than the atomic size, making i-AlPdMn a hyper-brittle material.
Fracture surfaces of i-AlPdMn were measured by P. Ebert and coworkers in Jülich (Germany). The present analysis of their experimental work shows: (i) a self similar behavior from 0.1 nm up to ξ = 2.3 nm, this last value being a good estimate of the process zone size. The cluster size (0.9 nm diameter) being within this range appears as an irrelevant length scale. (ii) the surface anisotropy allows determining the direction of the crack front propagation (iii) once the fracture axis (x,z) are known, the 2-d analysis shows a Family-Vicsek scaling that is found independent of the very nature of the material (see Fig.2):
 with
with 
Ph. Ebert, M. Feuerbacher, N. Tamura, M. Wollgarten, and K. Urban, Phys. Rev. Lett. 77, 3827 (1996).
Ph. Ebert, F. Kluge, M. Yurechko, B. Grushko and K. Urban, Surface Science, 523, 298 (2003).
•  Systèmes complexes et transition énergétique › Statistical physics in mechanics
Systèmes complexes et transition énergétique › Statistical physics in mechanics
• Laboratory of Physics and Chemistry of Surfaces and Interfaces • Service de Physique et Chimie des Surfaces et des Interfaces
• Laboratory of Nano-Objects and Complex Systems (LNOSC) • GMT-MSIN : Modélisation des Surfaces Interfaces et Nanostructures












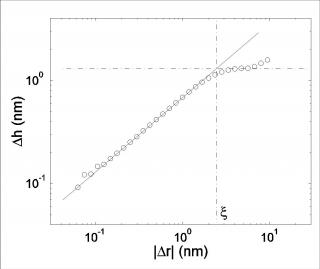
 with ξ = ~0.8.
with ξ = ~0.8.
