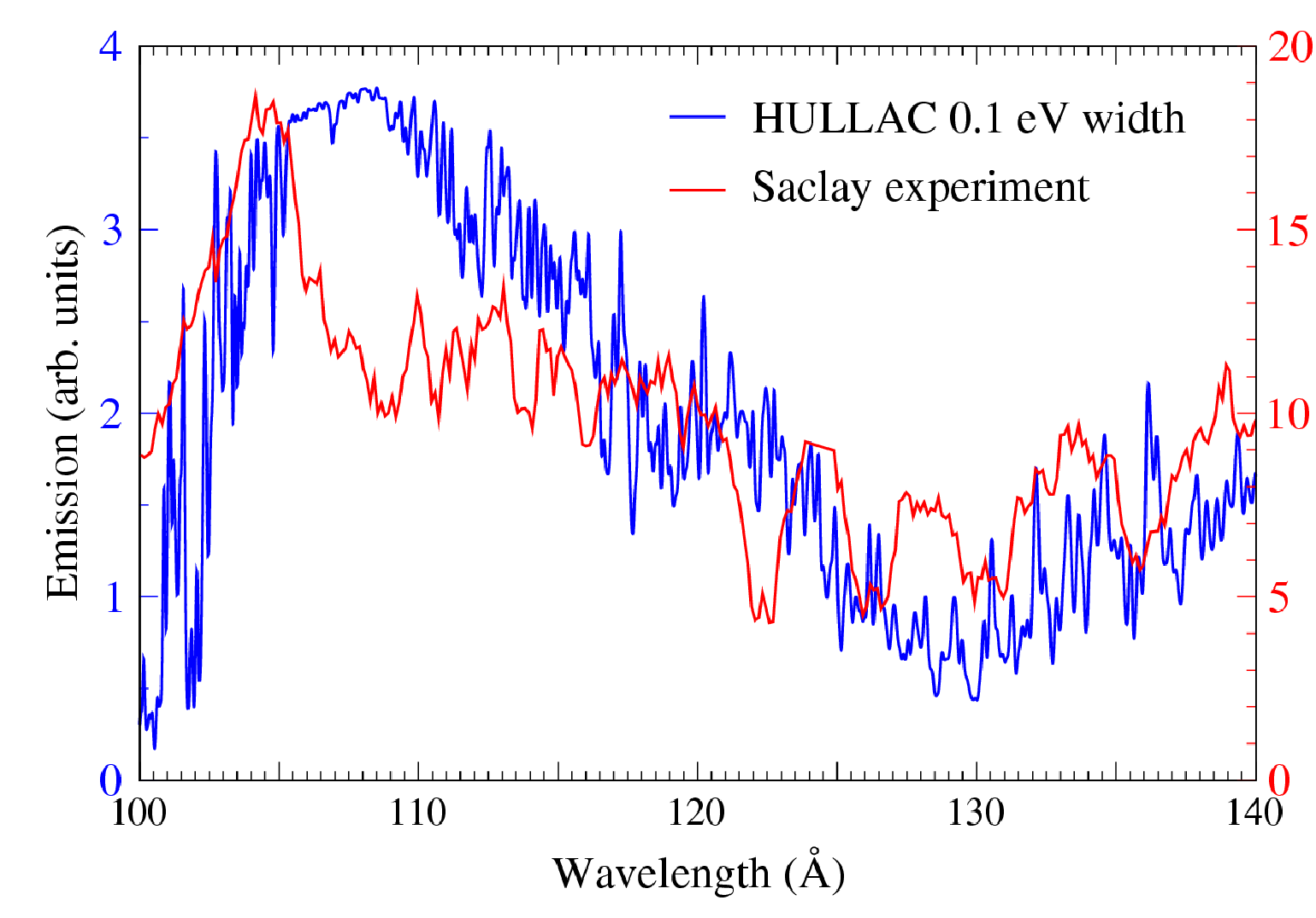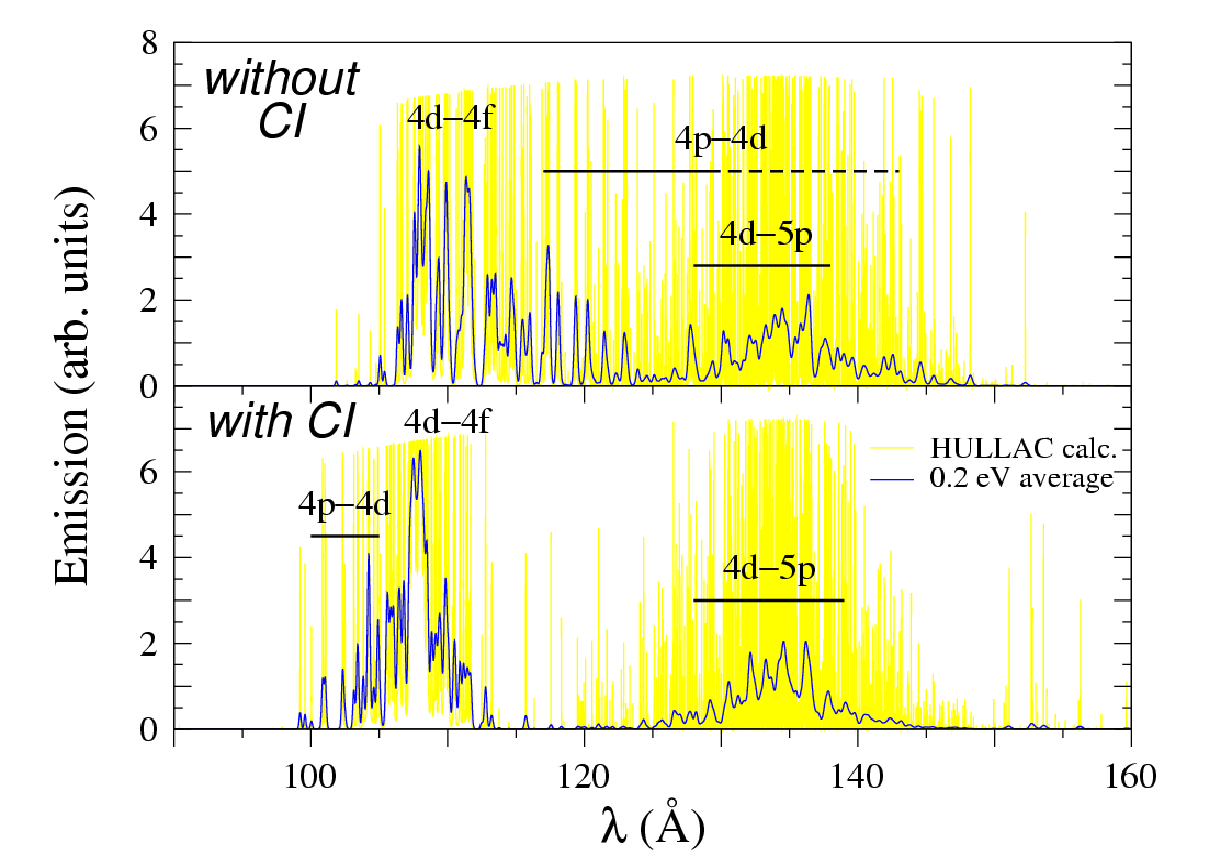
Figure 2: Emission of a xenon 10+ plasma at temperature 30 eV computed with HULLAC code: configuration interaction effect.
To go beyond the atomic formalism of auto-coherent central-field type, we have used the relativistic parametric potential code HULLAC, developed by Bar-Shalom and coworkers [7]. This code allows one to account for configuration interactions, particularly relevant for Dn = 0 transitions (as 4p – 4d or 4d – 4f) and for doubly excited states. It is available as a series of modules and determines for each detailed level its energy, wave-function, bound-bound radiative transition and autoionization probability, and if necessary cross-sections for collisional ionization, excitation and photoionization. A particularly important effect in ionic spectroscopy illustrated by fig. 2 is the configuration interaction (CI). Explicitly, one of the important processes in Xe10+ is associated to the transition between 4s2 4p6 4d6 and 4s2 4d5 4f configurations (the core with closed n = 1, 2, and 3 shells is omitted); but this transition is correctly described only if one considers that the excited state is mixed notably to the configurations 4p5 4d6 et 4p6 4d5 np. Such an effect shifts the levels of the band centered around 120 Å towards 100–110 Å and shrinks this band. In some cases, CI may also make allowed dipolar electric transitions that would be forbidden in a single-configuration one-active-electron description. One will notice however that all lines are not equally affected by CI: the group of 4d–5p lines around 135 Å is weakly shifted when CI is accounted for.