
Laurent PONSON, Daniel BONAMY, Elisabeth BOUCHAUD, Claude GUILLOT,
Coll: Harold AURADOU and Jean-Pierre HULIN (Laboratoire FAST, Université d’Orsay, France),
Guillaume MOUROT and Stéphane MOREL (Laboratoire LRBB, Université de Bordeaux, France)
The morphology of fracture surfaces is a signature of the complex damage and fracture processes occurring at the microstructure scale that lead to the failure of a given heterogeneous material. Since the pioneering work of Mandelbrot /1/, a large amount of studies have shown that crack surface roughening exhibits some universal scaling features: Fracture surfaces are self-affine over a wide range of length scales. In other words, the height-height correlation function Δh(Δr) =<(h(r+Δr)-h(r))2>1/2 computed along a given direction is found to scale as Δh ~ (Δr)ζ where ζ is the roughness exponent. This exponent was found to be weakly dependent on the nature of the material and on the failure mode with ζ~0.8 (see e.g. /2/ for a review).
In order to investigate possible anisotropy of fracture surfaces in heterogeneous materials, we computed the height-height correlation function along the direction of crack propagation (x-direction) and the direction of the crack front (z-direction). Four different materials with four different characteristic length scales of the microstructure were investigated: silica glass, aluminum alloy, mortar and wood. They were broken using four different types of fracture tests and the fracture surfaces were scanned by three different techniques. In all these different materials/failure modes, profiles were found to be self-affine in both directions, but with two different roughness exponents, namely ζ~ 0.75 along the crack front and β~ 0.6 along the direction of crack growth /3/4/.
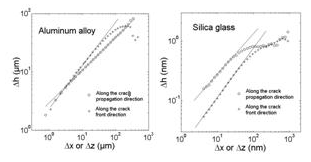
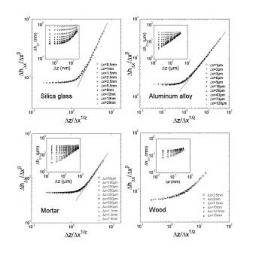
The insets show the variation of the 2D height-height correlation function Δh with Δz for various values of Δx for amorphous silica, aluminium alloy, mortar and wood. The data collapse was obtained from Equation (1) using ζ=0.75, β=0.6, Z=ζ/β=1.25.
To fully characterize the scaling properties of the fracture surfaces, we then computed the 2D height–height correlation functions defined as Δh(Δz, Δx) =<(h(z+Δz, x+Δx)-h(z,x))2>1/2. This function was shown /3,4/ to take a peculiar form, refered to as Family-Viseck scaling /5/:
 with
with  (1)
(1)
This 2D description involves the two independent scaling exponents ζ and β defined above. Those were shown to correspond respectively to the roughness exponentand the growth exponentintroduced in interface growth problems /6/. A third exponent – the dynamic exponent Z– must be introduced. As expected for Family–Vicsek scaling /5/, this last exponent is shown to be equal to the ratio of the two others, Z=ζ/β. The three exponents were found to be ζ=0.75, β =0.6 and Z= ζ/β=1.2 independent of the considered material, of the failure mode and of the crack growth velocity over the whole range from ultra-slow stress corrosion fracture (picometer per second) to rapid failure (few hundreds meters per second). They are therefore conjectured to be universal.
These observations enable a discussion on the various competing models developed to capture the scaling properties of fracture surfaces /7-10/. The anisotropy clearly evidenced in the scaling properties of fracture surfaces cannot be captured by static models such as percolation-based models /7/. On the other hand, such Family-Viseck scaling is reminiscent of what is observed in kinetic roughening models /6/. This provides a rather strong argument in favor of models such as the ones proposed in Refs. /8-10/ which derive the morphology of the fracture surfaces from Langevin-type equations with elastic interaction terms and annealed disorder. However, it should be emphasized that these models fail to reproduce quantitatively the exponents observed.
Finally, it is worth mentioning that the scaling properties exhibited by fracture surfaces may have interesting expertise applications. It allows one indeed to determine the direction of crack propagation from the analysis of post-mortem fracture surfaces and, thus, to reconstruct the history of the processes that have led to the failure of the structure.
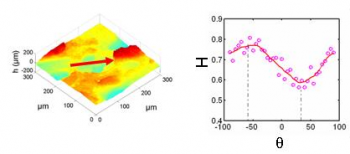
Determination of the direction of crack growth from self-affine roughness analysis. Top: fracture surfaces where the direction of crack growth is a priori unknown. Bottom: Variation of the effective Hurst exponent H measured along a direction making an angle θ with the scan direction. The minimum (resp. maximum) coincides with the direction of crack propagation (resp. the direction of the crack front), that can then be inferred (thick red arrow in left image).
REFERENCES:
[1] B. Mandelbrot, D.E. Passoja and A.J. Paullay, Nature 308, 721 (1984)
[2] E. Bouchaud, J. Phys. Condensed Matter 9, 4319 (1997)
[3] L. Ponson, D. Bonamy, E. Bouchaud, Phys. Rev. Lett. 96 035506 (2006)
[4] L. Ponson, D. Bonamy, H. Auradou, G. Mourot, S. Morel, E. Bouchaud, C. Guillot and J. P. Hulin,
Int. J. Fract. 140, 27 (2006)
[5] F. Family and T. Viseck, Dynamic of Fractal surfaces World Scientific (1991)
[6] A.L. Barabasi and H. E. Stanley, Fractal Concepts in Surface growth, Cambridge University Press (1995)
[7] A. Hansen and J. Schmittbuhl, Phys. Rev. Lett. 90, 045504 (2003)
[8] J.-P. Bouchaud, E. Bouchaud, G. Lapasset and J. Planès, Phys. Rev. Lett. 71, 2240 (1993)
[9] S. Ramanathan, D. Ertas and D.S. Fisher, Phys. Rev. Lett. 79, 873 (1997)
[10] S. Ramanathan, D.S. Fisher, Phys. Rev. Lett. 79, 877 (1997)
•  Systèmes complexes et transition énergétique › Statistical physics in mechanics
Systèmes complexes et transition énergétique › Statistical physics in mechanics
• Laboratory of Physics and Chemistry of Surfaces and Interfaces • UMR 3680 - Service de Physique de l'Etat Condensé (SPEC) • Service de Physique et Chimie des Surfaces et des Interfaces
• Laboratory of Nano-Objects and Complex Systems (LNOSC) • SPHYNX • GMT-MSIN : Modélisation des Surfaces Interfaces et Nanostructures
