
Daniel BONAMY,
Coll. : Mathieu RENOUF (LaMCoS, INSA de Lyon, Villeurbannes)
Frédéric DUBOIS, Pierre ALART (LMGC, Université Montpellier 2)
Bérengère DUBRULLE, Francois DAVIAUD (Groupe Instabilité & Turbulence, CEA/SPEC)
Pierre-Henri CHAVANIS (LPT, Université Paul Sabatier, Toulouse)
Absence of thermal agitation and the dissipative nature of the interaction between the constituent macroscopic particles set granular matter apart from conventional gases, liquids or solids. They can e.g. flow like liquids, but under given conditions jam and resist to external shear stress without deforming, like solids - the most spectacular manifestation occurs during avalanches when a thin layer of grains starts to roll at the surface of the packing, most of the grains remaining apparently static. This solid/liquid duality makes dry granular media not easy to describe.
To find out the constitutive laws of dense granular flows, we investigated two-dimensional steady surface flow of cohesionless disks in a rotating drum through nonsmooth contact dynamics simulations /1/. Profiles of volume fraction, translational velocity, rms velocity, strain rate, and stress tensor Σ are measured at the midpoint along the length of the surface-flowing layer, where the flow is generally considered as steady and homogeneous. Analysis of these data and their interrelations suggest that the inertial number I (defined as the ratio between the typical time of deformation and the typical time of confinement) is the relevant dimensionless parameter to describe the transition from the quasistatic part of the packing to the flowing part. Constitutive laws relating the components of the stress tensor to the inertial number were determined /1/.
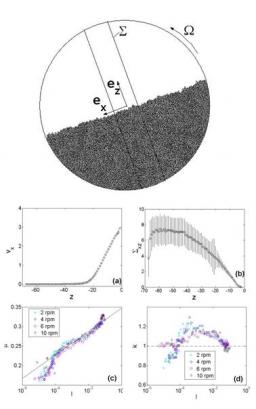
Top: Typical snapshot of the steady flows in the simulated 2D rotating drum. Bottom, a: Typical velocity profile . (b): Shear stress profile &Sigma:xz, both measured within S. Error bars correspond to a 99% confident interval. Calling d the mean diameter of grains, ρ0 their density and g the gravity constant, all distances, times, velocities and stresses are given in units of d,(d/g)1/2, (gd)1/2 and ρ0gd respectively. (c) and (d): Resulting constitutive laws relating the ratios μ=Σxz/Σzz and k= Σxx/Σzz to the inertial number respectively.
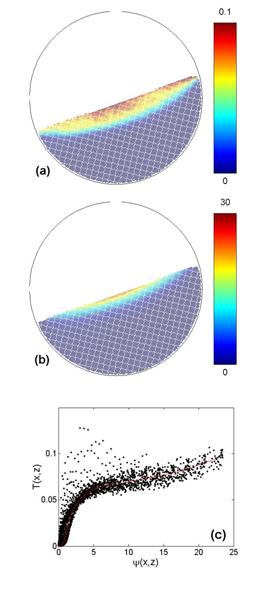
(a) Typical field of granular temperature T and (b) field of stream function Ψ (Ω=6rpm). Calling d the mean diameter of grains, ρ0 their density and g the gravity constant, all distances, times, velocities and stresses are given in units of d,(d/g)1/2, (gd)1/2 and ρ0gd respectively. According to the theory, all these fields can be fully described from the knowledge of two functions that relate the granular temperature, the vorticity and the stream function. We checked these predictions on the simulated rotating drum and determined these two functions. (c): the function relating the granular temperature to the stream field.
The effective friction μ= Σxz/Σzzwas found to increase logarithmically with I, independently of the rotating speed Ω. This relation matches quantitatively the one observed in other geometries (see e.g. /2/). On the other hand, the ratio k= Σxx/Σzzis found (i) to be significantly different from k=1 (in contrast to what was observed in the other geometries see e.g. /2/) and (ii) to depend also on the flow rate. This function k(I,…) was shown to be the one responsible for the flow localization within a thin layer at the surface. The shape of this function as well as its dependency with the flow rate lead us to conjecture that this ratio encodes the structure of the percolated network of grains in extended contact with each others – arches network. This picture is broadly consistent with non-local models based on the coexistence of particle chains and fluid-like materials /3/. This makes inoperative the classical methods used to relate the constitutive laws to the microscopic grains behaviour.
We then considered alternative approaches inspired from the modelling of turbulent fluids. In that case, the challenge is to relate the Reynolds stresses, based on small scale fluctuations, to large scale or time averaged quantities. A new way to tackle this problem was recently suggested /4/, through the consideration of non-linear steady solution of the Euler equations, thereby disregarding any non-universal effects induced by (large scale) forcing and (small scale) dissipation. We generalized this method to the case of dense granular flow assuming that in steady states, forcing and dissipation equilibrates locally /5/. As a result, we obtained a full characterization of the steady state through two general functions that relate granular temperature, vorticity, and stream function. We checked successfully these predictions on the steady surface flows observed in the simulated rotating drum. We are now developing a methodology to derive a “thermodynamic” of these steady states using a formalism derived from equilibrium statistical mechanics, in a spirit similar to the one applied in turbulent fluids modelling /6/.
•  Systèmes complexes et transition énergétique › Physique statistique et systèmes complexes
Systèmes complexes et transition énergétique › Physique statistique et systèmes complexes  Systèmes complexes et transition énergétique › Statistical physics in mechanics
Systèmes complexes et transition énergétique › Statistical physics in mechanics
• Laboratory of Physics and Chemistry of Surfaces and Interfaces • Service de Physique et Chimie des Surfaces et des Interfaces
• Laboratory of Nano-Objects and Complex Systems (LNOSC) • GMT-MSIN : Modélisation des Surfaces Interfaces et Nanostructures
