Service de Physique de l'Etat Condensé
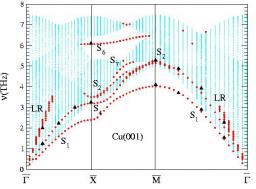
Calculated frequency spectrum of phonons for the low index surface Cu(100). Experimental points are represented by full triangles.
We have derived an N-body semi-empirical potential for FCC Cu which has some similarity with the so-called tight-binding second moment potential. However it improves the numerical values of the surface energies and gives the best results when the interactions are cut off between the second and third nearest neighbours. In particular this cut-off produces atomic relaxations at low index surfaces in good agreement with experiments. This has important consequences since any calculation of the phonon spectrum starts from the determination of the equilibrium atomic structure and the variation of the interatomic distances modifies the corresponding force constants. Its transferability is checked on a detailed study of the low index surfaces (111), (100) and (110).
Then it is applied to the determination of the surface projected phonon dispersion curves of a set of vicinal surfaces with increasing terrace widths and the results are compared with existing experimental data. The localized and resonant vibrational states can be identified by using a localization criterion on the first layers and are discussed in more details by means of the local spectral densities with a given value of the component of the wave vector parallel to the surface, k//. We have also calculated the mean square displacements on specific atoms. Finally, the vibrational free energy and its contribution to the free energy of the steps, as well as to step-step interactions due to phonons, are also derived. Références C. Barreteau, F. Raouafi, M.C. Desjonquères and D. Spanjaard. The phonon spectra and vibrational thermodynamical properties of Cu vicinal surfaces. Surf. Sci. 519, 15-32 (2002).
Calculated frequency spectrum of phonons for the vicinal surface Cu(211). Experimental points are represented by full triangles.
• 
Les archives de l'IRAMIS et du DRECAM / Archives of DRECAM and IRAMIS › Matériaux, surfaces et nanostructures
• Service de Physique et Chimie des Surfaces et des Interfaces • Laboratory of Physics and Chemistry of Surfaces and Interfaces
• GMT-MSIN : Modélisation des Surfaces Interfaces et Nanostructures • Laboratory of Nano-Objects and Complex Systems (LNOSC)
