La compréhension de la formation des solides amorphes, tels que les verres structuraux et colloïdaux, ou les empilements granulaires demeure un des défis majeurs de la matière condensée. Lorsque la température d’un liquide est abaissée, ou lorsque la densité d’un milieu granulaire est augmentée, tout en prenant soin d’éviter la transition de cristallisation, on constate un très fort ralentissement de la dynamique, beaucoup plus fort que ce à quoi on pourrait s’attendre pour une relaxation par activation individuelle des molécules ou grains. On parle alors de transition vitreuse, ou plus généralement de transition de jamming.
Ceci laisse supposer la présence d’un mécanisme de relaxation collectif, qui nécessiterait une énergie d’activation croissante avec l’abaissement de la température ou l’accroissement de la densité. Pour autant l’analyse des propriétés de la structure de ces systèmes ne révèle pas l’émergence d’un ordre facilement identifiable. Une question cruciale est donc de savoir si le ralentissement brutal de la dynamique est du à une véritable transition de phase et si oui de quelle nature, et pour quel paramètre d’ordre. Au-delà de cette question de nature fondamentale, il s’agit de savoir si un verre est un liquide qui ne coule pas, ou un solide sans ordre !
Ces dernières années, il a été suggéré que la transition puisse être d’origine purement dynamique. De nombreuses observations (expériences de molécules unique, mesure de susceptibilité diélectrique dans les liquides, diffusion de la lumière résolue en temps dans les colloïdes) et simulations numériques de systèmes modèles sont venues étayer cette idée. Néanmoins aucune évidence expérimentale directe de ces comportements collectifs, ni de leur dépendance avec le paramètre de contrôle n’avait encore été obtenu à ce jour.
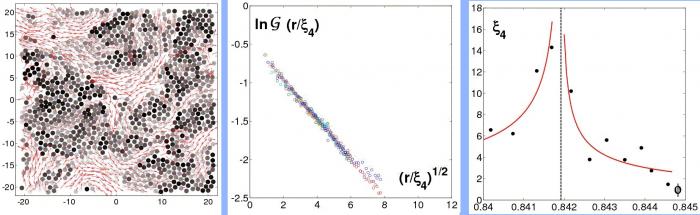
Nous avons obtenu la première indication expérimentale de la divergence à la fois d’une échelle de longueur et d’une échelle de temps dans la phase liquide comme dans la phase "jammée". Pour cela nous nous sommes intéressés à la dynamique d’une monocouche de disques bi-disperses vibrés horizontalement. Nous mesurons la pression à la paroi et enregistrons les trajectoires individuelles de quelques milliers de grains à l’aide d’une caméra CCD. Au-delà d’une certaine fraction surfacique, le système acquiert une composante statique de la pression, correspondante à la mobilisation de la friction entre les grains en contact. Le temps de relaxation correspondant à la réorganisation de ces contacts est fortement piqué au voisinage de Fc. La corrélation spatiale de la relaxation temporelle, mesurée par une fonction de corrélation à quatre points (deux temps et deux points d’espace), présente une loi d’échelle remarquable (Fig. 2) et la longueur associée un pic similaire à celui du temps de relaxation (Fig. 3). Ces échelles traduisent la formation de courants de relaxation intermittents et hétérogènes (fig. 1).
Ces résultats confortent le caractère critique de la transition, et donc son caractère universel. Ils ouvrent la perspective d’une étude systématique des propriétés rhéologiques de la couche granulaire au voisinage de la transition.
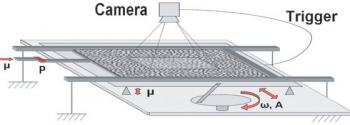
Dispositif expérimental : une monocouche de disques est soumise à des vibrations dans son plan. Le volume partiel occupé par les billes est finement contrôlé en déplaçant une des parois, sur laquelle la pression exercée est aussi mesurée. La caméra permet de suivre le déplacement individuel de chaque grain.
Référence :
Critical scaling and heterogeneous superdiffusion across the jamming/rigidity transition of a granular glass
F. Lechenault, O. Dauchot, G. Biroli and J. P. Bouchaud, European Physics Letters 83 (2008) 46003.
