•  Systèmes complexes et transition énergétique › Statistical physics in mechanics
Systèmes complexes et transition énergétique › Statistical physics in mechanics
• Laboratory of Physics and Chemistry of Surfaces and Interfaces • Service de Physique et Chimie des Surfaces et des Interfaces
• Laboratory of Nano-Objects and Complex Systems (LNOSC) • GMT-MSIN : Modélisation des Surfaces Interfaces et Nanostructures

Cindy Lynn ROUNTREE, Elisabeth BOUCHAUD
Coll: Mehdi TALAMALI, Damien VANDEMBROUCQ, (UMR CNRS/Saint-Gobain, Aubervilliers)
Stéphane ROUX (LMT, ENS-Cachan/CNRS-UMR 8535/Université Paris VI)
Rajiv KALIA (University of Southern California, Los Angeles, USA)
In order to understand the origin and nature of irreversible deformations in silica glass, we performed MD simulations of amorphous silica systems which are subjected to (1) a cyclic loading and unloading of the hydrostatic pressure and (2) a shearing force.
Simulations presented herein involve 12 independent 5184 atoms systems of amorphous silica. Amorphous silica was generated by heating β-cristobalite to 3200K and then quenching the molten system to 0K. At this point a conjugate gradient was run to relax the system. Afterwards the system was heated up to ambient temperature.
Subsequently, the effects of cyclic densification in 12 independent systems 5184 atoms each are examined. The systems are densified in a stepwise process to a peak point. Afterwards, the systems are expanded back out to (1) their initial volume; or (2) until the pressure is approximately 0GPa.
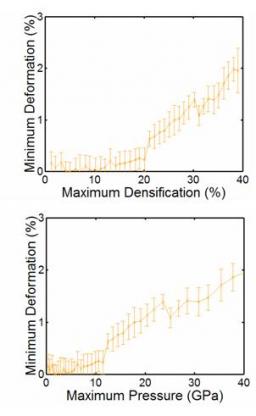
This process is repeated continuously by increasing slightly each time the value of the peak densification point. After the system reaches ~21% maximum densification, it was found to have a residual densification of ~0.6% (i.e. the system was unable to return to its original density, see figure 1). Similarly the pressure corresponding to peak densification was examined. Once the system exceeds ~12GPa, the system is found to have a residual densification (see figure 1). This 21% maximum densification and the 12GPa pressure define the onset of plasticity, in agreement with experimental values.
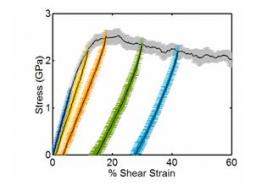
The effects of cyclic shearing in 12 independent systems 5184 atoms each are examined. The systems were initially sheared from 0% shear strain to 60% shear strain (see figure 2, black line, error bars in grey). As one can see up to about 5% shear strain the system experiences a linear elastic behavior. Also it is important to note that the shear modulus can be calculated in this linear region and is in good agreement with experiments. Afterwards the system enters into the non-linear elastic regime. The stress reaches a maximum around 15% at which point the stress begins to decrease slightly and the systems begins to flow.
Figure 2 also depicts the evolution of the shear strain when reversed: (1) from +5.91% to 0% shear strain (error bars in dark green); (2) from +11.91% to 0% shear strain (error bars in blue); (3) from +17.91% to 0% shear strain (error bars in yellow); (4) from +29.91% to 0% shear deformation (error bars in light green); (5) from +41.91% to 0% shear deformation (error bars in orange). When the shear is reversed at 5.91% shear strain, the stress from 5.91% strain to 0% strain depicts a virtual linear elastic behavior (i.e. it follows the initial loading curve shown with dark green error bars). At 0GPa stress the shear strain is 0%, hence when the system is unloaded from 5.91% strain it undergoes no permanent plastic deformation. When the shear is reversed at 11.91% shear strain, the stress from 11.91% strain to 0% strain depicts an anti-elastic behavior. Hence it does not follow the initial loading curve; however, at 0GPa stress the shear strain is ~0%. Thus the system does not undergo a permanent plastic deformation. Lastly the stress of a system was unloaded from 17.91% shear strain, 29.91% shear strain, and 41.91% shear strain. Each curve traces out its own unloading path, depending on the point where shear was reversed. When completely unloaded, the systems exhibit residual shear strain; about 3.5%, 14%, and 27% when unloaded from 17.91%, 29.91%, and 41.91% shear strain, respectively.


