L.I.O.N.S. : Small Angle X-Rays Scattering
 |
|
Available apparatus in the lab :
- A high sensitivity SAXS pinhole camera for soft condensed matter- USAXS
- WAXS
What is measured in a Small Angle X-ray Scattering (SAXS) ?
S. Lyonnard, O. Spalla, F. Testard, F. Né, O. Taché1 - What is measured in a Small Angle X-ray Scattering (SAXS) experiment ?
2 - What does "q-range" mean ?
3 - Porod's law: specific surface and interface
4- Form factor P(q) : size and shape of particles
5 - Structure factor S(q): interactions between particles
6 - Technical potential of investigation
7 - Absolute intensity
8 - Usefull Links
1 - What is measured in a Small Angle X-ray Scattering (SAXS) experiment ?
X-rays
are used to investigate the structural properties of solids, liquids or gels.
Photons interact with electrons, and provide information about the fluctuations
of electronic densities in heterogeneous matter. A typical experimental set-up
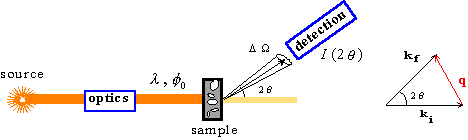
is shown on Figure 1: a monochromatic beam of incident wave vector ki is selected and falls on the sample. The scattered intensity is collected
as a function of the so-called scattering angle 2q. Elastic interactions are characterised by zero energy transfers,
such that the final wave vector kf is equal in modulus to ki. The relevant parameter to analyse the interaction is the momentum
transfer or scattering vector q=ki-kf, defined by q=(4p/l)sinq. The standard unit for q is Å-1.
 F
F
igure 1: Schematic view of a typical scattering experiment.
The scattered intensity I(q) is the Fourier Transform of g(r), the correlation function of the electronic density r(r), which corresponds to the probability to find a scatterer at position r in the sample if another scatterer is located at position 0: elastic x-ray scattering experiments reveal the spatial correlations in the sample. Small angle scattering experiments are designed to measure I(q) at very small scattering vectors q»(4p/l)q, with 2q ranging from few micro-radians to a tenth of a radian, in order to investigate systems with characteristic sizes ranging from crystallographic distances (few Å) to colloidal sizes (up to few microns).
· Electronic contrast. The number of photons scattered by one sample is proportional to its total volume V and to its electronic contrast. In the simple case of a binary system for instance, like scattering objects of density r1 embedded in a solvent of density r2, the electronic contrast is Dr=r1-r2 (e.Å-3 or cm-2). The higher the contrast between particles and solvent, the more intense the scattered signal.
![]()
· Absolute intensity. The experimental intensity is usually fitted in order to determine the density r(r), the size, the shape and the internal structure of one elementary scatterer, as well as the structure and the interactions between scatterers. The determination of physical quantities, such as molecular weight, particle volume, specific surface or osmotic compressibility, is feasible only if I(q) is measured on absolute scale. As shown on figure 1, part of the incident beam is absorbed in the material. The number of photons scattered in the solid angle DW in the direction 2q have to be normalised with respect to the number of photons transmitted through the sample. This implies to control several parameters: the sample thickness e (cm) and transmission T, the incident flux of photons f0 (photons/s) and the solid angle of one pixel of the experiment DW. The absolute intensity can then be obtained in absolute units (cm-1):
2 - What does "q-range" mean ?
A
typical small angle scattering intensity profile is shown on figure 2. The intensity
is plotted versus q, in the range qmin-qmax defined by
the experimental set-up and usually fixed by geometric limitations.
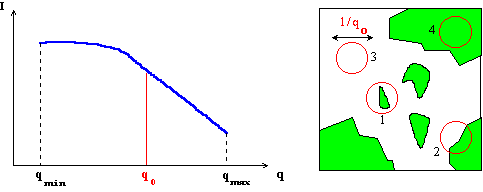
Figure 2: Left: Example of scattering intensity profile measured between qmin and qmax. Right: Binary sample and "q-window" corresponding to a measurement at a given q0. The contrast is equal to zero in cases 3 and 4, and different from zero in cases 1 and 2.
Intuitively, a measurement made at a given q0 allows to investigate the density fluctuations in the sample on a distance scale D0=2p/q0. It is equivalent to observe the system through a 2p/q0 diameter "window" in real space, as shown in figure 2b. The red circle is the observation window. A scattering signal is observed if the contrast Dr inside the circle is different from zero. To study objects much smaller or much larger than D0=2p/q0, another "window" has to be chosen. The smallest (largest) observation window is given by Dmin(max)=2p/qmax(min): it determines the size of the smallest (biggest) particles that can be observed with the instrument.
The q-range of small angle experiments is usually divided into three main domains:
| Example: suspension of identical particles. |
High q domain: The window is very small: there is a contrast only at the interface between the two media. This domain called the Porod's region, gives information about the interfaces present in the sample. Intermediary zone: The window is of the order of the "elementary bricks" in the systems. The form factor P(q) can be measured (size, shape and internal structure of one particle). Low q domain: When the observation window is very large, the structural order can be obtained: it is the so-called structure factor S(q), which allows to calculate the interactions in the system. |
3 - Porod's law: specific surface and interface
When two media are separated by a sharp interface, the scattered intensity follows an asymptotic law in the high q region: I(q)=Aq-4+B. This law is called the Porod's limit (and has more sophisticated expressions in the case of complicated interfaces). The asymptotic value, when the electronic contrast of the sample is known, and when the intensity is expressed in absolute scale, allows to calculate the specific surface S (in cm2/cm3) of the particles.
The q-range of validity of a Porod's law can cover several
decades, giving information about the average particle or hole sizes. When various
types of particles, with different characteristic scales, exist in the sample,
it is possible to measure two Porod's law observable at different scales, as
shown in the following example. A borosilicated glass is alterated and studied
as a function of water leaching time, in order to investigate the alteration
process. The initial glass before alteration can be represented as a two-media
system, with large grains distributed in the solvent. The scattering signal
shown in red is a Porod's law resulting from the sharp interface between the
solvent and the grain, ranging from 10-4 to 0.1 Å-1. When
the sample is alterated a second Porod's law appears at larger q: small pores
are created in each grain. It is the sharp interface pore-grain that gives rise
to this excess scattering. As the pore's size increases with time, the Porod
type behaviour after 8 weeks is shifted towards smaller q respect to the 2 weeks
alteration glass signal. In this particular case, measuring the intensity on
absolute scale is critical to calculate the pore's surface (and radius, if a
spherical shape is assumed), as well as the grain's surface.
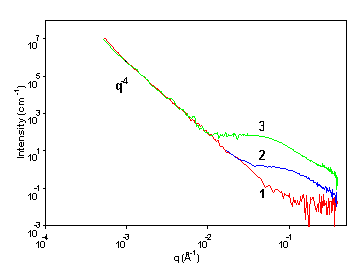
1 Non altered glass
2 Altered glass (2 weeks)
3 Altered glass (8 weeks)
Figure 3: USAXS on fine powder of borosilicated glasses :evolution of the glass water interfacial gel during corrosion induced by contact with pure water is evidenced by an increase of the SAXS signal at large angle, i.e. in a domain corresponding to 6nm. The low-q behaviour folllows a perfect Porod law giving the specific area of the wet powder sample.
4- Form factor P(q) : size and shape of particles
The size and the shape of “particles” are of fundamental interest to understand the microstructure of a heterogeneous material or complex fluid. Small angle X-ray scattering gives valuable information, providing that the contrast is sufficient. If the particles are of the order of one micron, these results can also be obtained by light scattering. If the system is complex (three different media for instance), it can be completed by neutron scattering, which offers the possibility of contrast variation methods.
Experimentally, form factors can only be measured in the dilute regime where particles can be considered as independent scatterers without any interactions. In this case, the intensity is directly proportional to:
ð the contrast Dr.
ð the volume fraction f and the volume of one particle VP.
ð the form factor of a single particle P(q).
· Elementary shapes. Form factors are easily calculated for spheres, cylinders, disks, rods, micelles, lamellas or Gaussian polymers, which are the basic shapes encountered in soft condensed matter. However, the only analytical expression is the sphere form factor that is represented on Figure 4.
· Example. The experimental intensity scattered by a diluted solution of silica spheres of radius R=3000 Å is shown above on figure 4. The experiment has been performed on our laboratory Bonse/Hart camera. The data are compared to the theoretical form factor P(Q) calculated by perfectly monodisperse spheres. Experimental data are smoothed compared to the model because of the instrument resolution (and some polydispersity). The location of the first minimum gives the radius of the particles, since at that point qR=4.5. A good fit is obtained in this case with R=3000 Å. The extrapolation of the absolute intensity at q=0 allows to calculate the volume fraction of particles in the solvent.
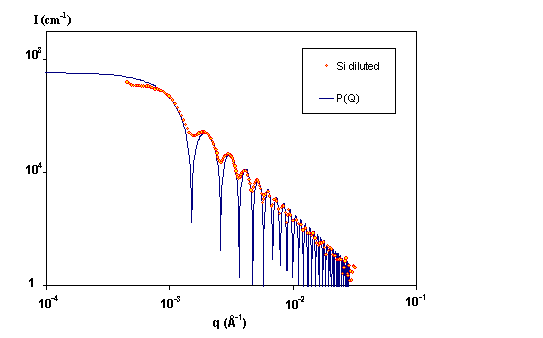
Figure 4: USAXS determination of the form factor of silica spheres. Desmeared data points compared to monodisperse homogeneous spheres.
5 - Structure factor S(q): interactions between particles
Complex systems are described through interaction potentials. Are the interactions attractive or repulsive, electrostatic or not? Is there any long range order in the system ? What is the effect of temperature, salt or pressure on the equilibrium? SAXS experiments combined with adapted models bring some answers, provided the structure factor S(q) can be extracted from the scattered intensity I(q).
For instance, in the case of centrosymmetric identical particles in solution, the signal due to one single particle can be dissociated from the signal arising from the interactions between particles. The intensity is then proportionnal to the product P(q)*S(q).
The limit S(q=0) gives the osmotic compressibility of the sample, but this quantity is only accessible if absolute intensities can be measured. When there is no interaction, as in the previous example of silica spheres in diluted regime, the structure factor is equal to 1 over the whole q-range. Repulsive electrostatic interactions appear between these charged silica spheres when one concentrates the sample. The experimental result is shown in Figure 5: at large q, where the "observation window" mainly shows the particle itself, the form factor of a sphere is predominant. The intensity profile in this region is identical to the one measured in the diluted regime. However, an interaction peak appears at small q, the position of which is related to the distance between neighbouring particles. The signal results from the product of P(q) and S(q).
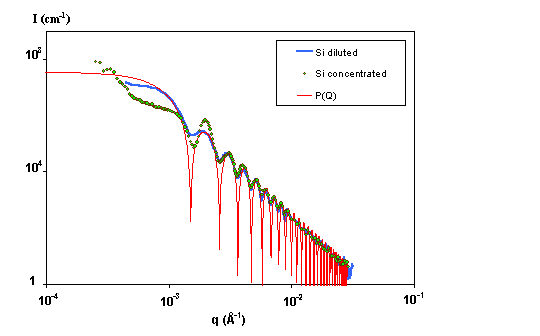
Figure 5: Experimental USAXS data on charged Silica spheres in interaction. The signal I(q) is decomposed in two terms : the form factor P(Q) and the structure factor S(Q).
6 - Technical potential of investigation
The three different (I,q) regions accessible with our cameras are drawn in different colours on figure 6, and compared to the USAXS performances at the ESRF. There is an overlap between the 2D cameras and the Bonse/Hart camera, which allows a good recovering of data on four decades in q and nine decades in intensity. The combination of the three instruments thus constitutes a powerful technical platform, with a high sensitivity and complementarity.
Some typical materials studied in soft condensed matter are located on the same (I,q) diagram: we routinely measure scattering from colloidal crystals at very small q, mesoporous materials at large q, or water and molecular liquids at very small intensities. We use pure water at room temperature as reference, since its absolutely scaled intensity is deduced from isothermal compressibility and thus well known: I=1.68 10-2 cm-1.
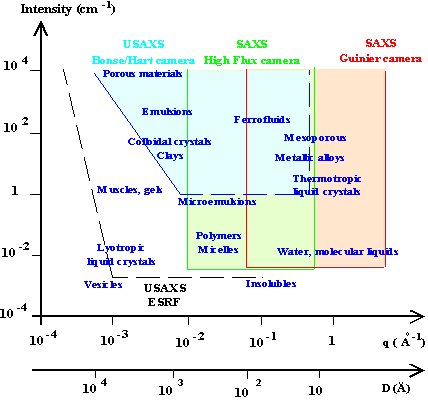
Figure 6: Intensity versus scattering vector : the technical platform, combining three different cameras, allow to measure signals from 3.10-4 Å-1 up to 2 Å-1, and intensities varying from few 10-2 to 104 cm-1. The D-scale gives the corresponding direct measure of characteristic sizes in the system: from few Å to few microns.
7 - Absolute intensity
Absolute intensities are experimentally very difficult to obtain, but crucial to quantify a system. We have shown how specific surfaces, for instance, can be extracted from Porod's law only if the intensity is given in absolute units (cm-1). Figure 7 illustrates for instance the case of TiO2 powders similar to those used in the Australian SYNROC project for waste storage. These materials are constituted by an assembly of hierarchical aggregates : the elementary bricks are 8 nm grains, which form aggregates of 100 nm, themselves contained in larger macroscopic aggregates. Experimentally, we have observed two Porod's limits corresponding to the two smallest sizes in the system. The use of two different cameras was necessary to cover the whole relevant q-range. We are showing on figure 7 the scattering in absolute units measured on the same sample, on the three cameras available at the laboratory. The measurements have been made independently one from the other: an excellent connection is observed between the three data sets. The shape of the signal, as well as the intensities, is identical. The first crystallographic Ti-Ti peak is observed at large q.
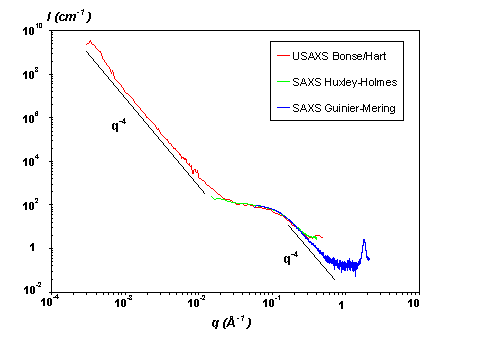
|
| Figure 7: Superposition of scattering data obtained on the three cameras on TiO2 powders. A schematic representation of the system is represented on the right. The red grains give rise to a Porod's law at large q. The specific surface of small and large grains can be calculated |
|
These results confirm the complementarity of the three machines, and the coherence of the measurements: absolute intensities are measured with a very good reliability on a large q-scale.
8 - Usefull links
EUROPEAN SCHOOL ON SCATTERING METHODS APPLIED TO SOFT CONDENSED MATTER" (Bombannes 2004)
Instrumentation for Small-AngleX-ray and Neutron Scattering and Instrumental Smearing Effects ( Jan SkovPedersen, Departmentof Chemistry, and iNANOInterdicsiplinaryNanoScienceCenter Universityof Aarhus)
GENERAL THEOREMS IN SMALL ANGLE SCATTERING (O. Spalla, CEA/DSM/DRECAM/SCM/LIONS)
Using scattering to investigate microemulsions (Th. Zemb, CEA/DSM/DRECAM/SCM)
ESRF ID2 High Brilliance Beamline