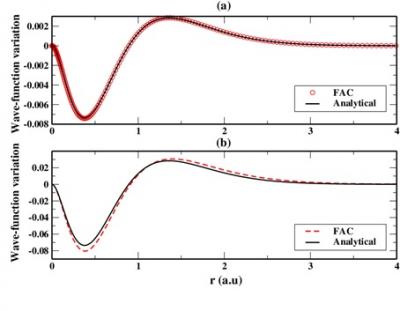
Figure 1. Density effect on the 3d3/2 wavefunction in Al 12+. Wavefunction variation due to the plasma environment effect. The calculation is performed within the uniform free-electron gas model with density with Ne=1023 e/cm3 (a) or 1024 e/cm-3 (b). The solid black curves come from analytical computations, the red curves are from numerical integration using FAC [Belkhiri 2013].
This activity is aimed at studying the effects related to the presence of other ions and free electrons on the energies and wave-functions of an ion in a plasma. It is based on an ion-sphere type approach and concerns mostly moderate-density and high-temperature plasmas.
The simplest hypothesis consists in considering that the free electrons form a uniform-density gas which screens the nucleus-electron Coulomb interaction. The “plasma potential” is then analytically defined [Weisheit1996]. One of the interests of this approach is that it allows analytical calculations in the case of hydrogen-like ions, using time-independent perturbation theory [Belkhiri2013]. One may provide expressions for the perturbed energy at first and second orders, which allows one to define the validity of this perturbation approach. One may also obtain wave-functions perturbed up to first order as well as dipolar-electric matrix elements or radiative rates at this same order. A comparison of analytical expressions to numerical computations is presented on Figure 1.
A more involved description of the environment effect accounts for the polarization of the free electron density by the nucleus. A semiclassical method similar to the one use to describe the Thomas-Fermi atom — using a statistical expression for electron density, ionic sphere neutrality and Poisson equation — allows one to get implicitly the free-electron density and the “self-consistent” plasma potential. The obtained density accounts for the polarization of free electrons by the nucleus. This self-consistent potential is provided by a numerical integration. Nevertheless for hydrogen-like ions one may provide an approximate analytical expression valid for any value of nuclear charge and electron density, provided that the current ion-sphere hypothesis holds [Poirier2015].
These plasma potentials have been included in the Flexible Atomic Code [Belkhiri2013]. They allowed us to compute energy shifts, radiative and collisional rate corrections [Belkhiri2014, Belkhiri 2015]. An example of radiative rates including this effect in a helium-like ion is displayed on Figure 2.
Reféeences :
- [Weisheit1996] J. Weisheit, Atoms in Plasmas (in Atomic, Molecular and Optical Physics Handbook, G. W. F. Drake ed., AIP Press, Woodbury NY, 1996).
- [Belkhiri2013] “Density effects in plasmas: detailed atomic calculations and analytical expressions”, M. Belkhiri, M. Poirier, High Energy Density Phys. 9 609 (2013).
- [Belkhiri2014] “Analysis of density effects in plasmas and their influence on electron-impact cross-sections”, M. Belkhiri and M. Poirier, Phys. Rev. A 90 062712 (2014).
- [Belkhiri2015] “Influence of the plasma environment on atomic structure using an ion-sphere model”, M. Belkhiri, C. J. Fontes, and M. Poirier, Phys. Rev. A 92 032501 (2015).
- [Poirier2015] “A study of density effects in plasmas using analytical approximations for the self-consistent potential”, M. Poirier, High Energy Density Phys. 15 12 (2015).

Figure 2. Density effect on the radiative rates 1s4p 3PJ ->
1s4s 3S1 in Al11+.
The computation is done with FAC including a plasma potential, either of uniform electron gas type (UEGM), or Thomas-Fermi type (TF) [Belkhiri 2014]. The transition rate is plotted as a function of the spatially averaged free-electron density.











 Institut Rayonnement Matière de Saclay
Institut Rayonnement Matière de Saclay