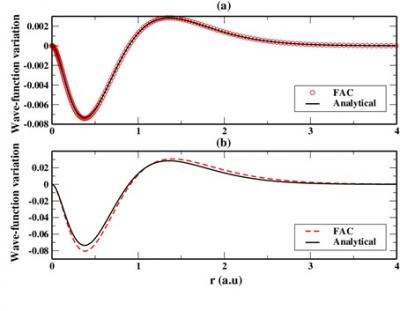
Fig 1. Effet de densité sur la fonction d’onde 3d3/2 de Al 12+. Variation de la fonction d’onde due à l’environnement plasma. Le calcul est fait dans un modèle de gaz d’électrons libres uniforme de densité Ne, avec Ne = 1023 cm-3 (a) et 1024 e/cm-3 (b). Les courbes noires en trait continu résultent d’un calcul analytique, les courbes rouges d’une intégration numérique avec le code FAC [Belkhiri 2013].
Cette ligne de recherche a pour objet l’étude des modifications apportées par la présence des autres ions et des électrons libres sur les énergies et les fonctions d’onde d’un ion dans un plasma. Elle est fondée sur une approche de type « sphère ionique » et s’applique principalement aux plasmas chauds et peu denses.
L’hypothèse la plus simple consiste à considérer que les électrons libres forment un gaz de densité uniforme qui « écrante » l’attraction Coulombienne électron-noyau. Le « potentiel plasma » est alors défini analytiquement [Weisheit1996]. L’un des intérêts de cette approche est qu’elle permet des calculs analytiques dans le cas d’ions hydrogénoïdes, dans le cadre de la théorie des perturbations indépendantes du temps [Belkhiri2013]. Il est ainsi possible de donner des expressions de l’énergie perturbée à l’ordre 1 et 2, ce qui permet de définir la validité de la théorie perturbative. On peut aussi calculer les fonctions d’onde perturbées à l’ordre 1 ainsi que des éléments de matrice dipolaires ou des taux radiatifs perturbés au même ordre. Une comparaison de ces formes analytiques à un calcul numérique est présentée sur la figure 1.
Une description plus élaborée tient compte de la polarisation de la densité des électrons libres par le potentiel du noyau. Une méthode semi-classique analogue à celle utilisée pour l’atome de Thomas-Fermi — utilisant une expression statistique de la densité électronique, la neutralité de la sphère ionique et l’équation de Poisson — permet de calculer de manière implicite la dépendance radiale de la densité d’électrons libres et le potentiel plasma « auto-cohérent ». La densité calculée prend en compte l’effet de polarisation des électrons libres par le noyau. Ce potentiel plasma « auto-cohérent » est donné par une intégration numérique. Néanmoins il est possible pour les ions hydrogénoïdes d’en donner une expression analytique approchée utilisable pour toutes valeurs de la charge du noyau et de la densité électronique, à condition que l’approximation de sphère ionique soit acceptable [Poirier2015].
Ces potentiels ont été inclus dans le code FAC [Belkhiri2013]. Ils ont permis de calculer des déplacements d’énergie, des corrections aux taux radiatifs et collisionnels [Belkhiri2014, Belkhiri2015]. Un exemple de calcul de taux radiatif incluant cet effet de densité dans un ion héliumoïde est présenté sur la figure 2.
Références :
- [Weisheit1996] J. Weisheit, Atoms in Plasmas (in Atomic, Molecular and Optical Physics Handbook, G. W. F. Drake ed., AIP Press, Woodbury NY, 1996).
- [Belkhiri2013] “Density effects in plasmas: detailed atomic calculations and analytical expressions”, M. Belkhiri, M. Poirier, High Energy Density Phys. 9 609 (2013).
- [Belkhiri2014] “Analysis of density effects in plasmas and their influence on electron-impact cross-sections”, M. Belkhiri and M. Poirier, Phys. Rev. A 90 062712 (2014).
- [Belkhiri2015] “Influence of the plasma environment on atomic structure using an ion-sphere model”, M. Belkhiri, C. J. Fontes, and M. Poirier, Phys. Rev. A 92 032501 (2015).
- [Poirier2015] “A study of density effects in plasmas using analytical approximations for the self-consistent potential”, M. Poirier, High Energy Density Phys. 15 12 (2015).
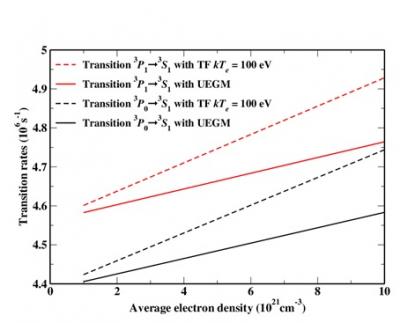
Figure 2. Effet de densité sur les taux radiatifs 1s4p 3PJ -> 1s4s 3S1 de Al 11+. Le calcul est fait avec le code FAC incluant un potentiel plasma, soit de type gaz d’électrons libres uniforme (UEGM), soit de type Thomas-Fermi (TF) [Belkhiri 2014]. Le taux de transition est représenté en fonction de la densité d’électrons libres moyennée spatialement.












