Our group has made very significant contributions to the understanding and control of plasma mirrors in the last decade, becoming one of the worldwide leaders on this topic. Our main results are summarized below.
Plasma mirrors for contrast improvement
High-order harmonic generation: basic mechanisms
Properties of high order harmonics from plasma mirrors
Generation of attosecond light pulses
Interaction with structured targets and transient plasma gratings
Plasma mirrors as injectors of electrons in UHI laser fields
Plasma mirrors for contrast improvement
We started working on this topic in 2002, when we investigated the use of plasma mirrors as ultrafast self-triggered optical switches [Dou04], to improve the temporal contrast of femtosecond laser pulses by orders of magnitude and avoid the deleterious effect of the temporal pedestal of UHI laser on solid targets [Mon04]. We were the first group to permanently install a double plasma mirror (see picture 1) system for contrast improvement on our TW-class laser [Lev07,Tha07]. We thus routinely obtained temporal contrasts better than 1010 on the 100 ps time-scale, which enabled us to perform some of the first ultrahigh-intensity experiments on solid targets in very well controlled conditions.

Picture 1: picture of a double plasma mirror just after a laser shot. While the plasma surface remains optically flat during a femtosecond laser pulse, and hence does not degrade the laser beam, jets of plasmas and debris are emitted long after this pulse is gone.
High-order harmonic generation: basic mechanisms
Thanks to this improved controlled of the interaction, we could start investigating the generation of high-order harmonics that occurs when very intense fs laser pulses reflect on plasma mirrors. We first identified a new generation mechanism, called coherent wake emission (CWE) [Que06], where the harmonic emission results from collective electron oscillations in the dense plasma, triggered by attosecond bunches of fast electrons injected by the laser field from the plasma surface into its bulk. CWE remains efficient for laser intensities down to a few 1015 W/cm2. This is an ubiquitous mechanism in all harmonic generation experiments on plasma mirrors.
By increasing the peak intensity in our experiments, we were then able to simultaneously observe harmonics due to the CWE and Relativistic oscillating mirror (ROM) mechanisms (see figure 1) [Tha07]. A remarkable feature is that these two families of harmonics can be very clearly distinguished in experiments, in particular through to their different spectral widths and divergences.
Figure 1: Raw images of HHG spectra, obtained on a plastic target at a laser intensity of 8.1018W/cm2. Harmonics below the 15th are due to CWE, and those above to ROM, leading to a striking difference in spectral width. From [Tha07].
Properties of high order harmonics from plasma mirrors
To explain these striking differences observed on the harmonics beams resulting from the two generation mechanisms, we then investigated the properties of these beams both experimentally and theoretically –in particular their phase properties (e.g. their spatial and temporal phase). We described how the phase of CWE harmonics depends on the laser intensity, leading to significant spatial and temporal phases of these harmonics, which significantly affect their properties [Que08,Tha08]. Later on, we investigated the phase properties of ROM harmonics, which are mostly determined by the deformation of the plasma mirror surface see figure 2), resulting from the inhomogeneous radiation pressure and ponderomotive force exerted by the incident laser field [Vin14]. The different dependences of the phase of these two types of harmonics on laser intensity explain why their properties are observed to be so different in experiments. A review of all these results is provided in [Tha10].
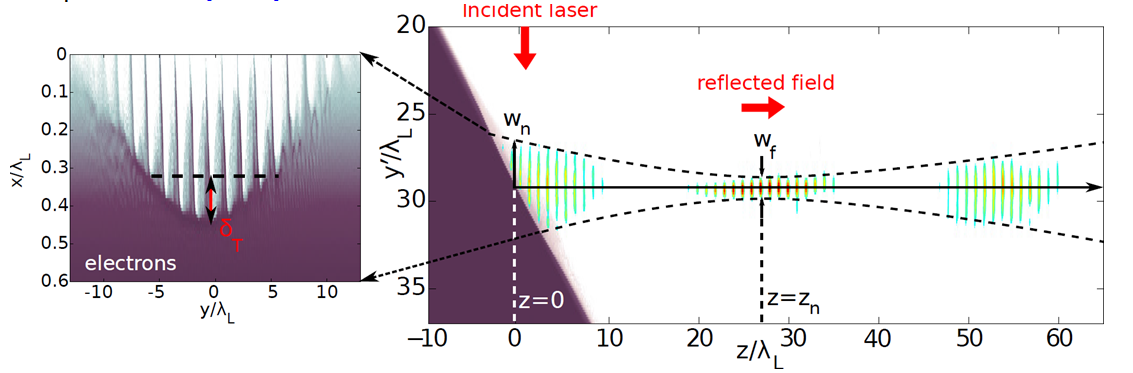
Figure 2: Focusing of high order harmonics by a curved relativistic plasma mirror in a 2D PIC simulation. The laser-induced curvature of the plasma mirror surface tends to focus the reflected light in front of the plasma mirror. The right panel shows a spatial map of the plasma electron density ne(x,y) at the maximum of the laser pulse in dark red scale. A zoom on the surface is shown in the left panel. The multicolor map shows the intensity of the train of attosecond pulses obtained by filtering ROM harmonics from order 4 to 8, at three different times during its propagation away from the PM. Focusing of this train in vacuum, in front of the plasma mirror surface, is clearly observed.
A part of our work has focused on the control of the dynamics of plasma mirrors, and of the resulting attosecond light pulses and high-order harmonics. We have first shown that this dynamics can be controlled through the phase properties of the driving laser [Que08]. In particular, shaping the spatial phase of the laser beam has a direct effect on the divergence of the harmonic beams produced on plasma mirrors. This makes it possible to compensate the effect of the intensity-dependant phase. A similar effect occurs in the time-domain, leading to a control on the spectral widths of individual harmonics.
In collaboration with the PCO group of LOA, we have then shown that the emission times of CWE attosecond pulses can be varied by changing the Carrier-Envelop relative Phase (CEP) of a few-cycle laser pulse [Bor12]. This has been the first plasma physics experiment with a controlled CEP.

Figure 3: effect of the CEP phase of harmonic spectrum from plasma mirrors. Artistic view of the CWE harmonic spectrum generated by a few-cycle laser pulse (5 fs duration), as a function of its Carrier-Envelop relative Phase (used here as a polar coordinate). From cover of Nature Physics, May 2012
More recently, we have obtained the first direct and quantitative experimental evidence of the influence of the scale length of the density gradient at the plasma surface on the harmonic signal [ Kah13]. CWE was found to be optimized from extremely short density gradients (λ/50), while ROM is maximal for density gradients of about λ/10. This parameter is also found to have to strong effect on the harmonic divergence [Vin14].
Generation of attosecond light pulses
Since the dynamics of plasma mirrors is influenced by the phase of the driving laser field, shaping this phase in space-time can provide a very fine control of the emission of attosecond light pulses. This is the idea underlying the attosecond lighthouse effect, which we proposed in [Vin12]. The idea is to induce an ultrafast rotation of the propagation direction of the laser field at focus, by inducing a slight spatial chirp. When such a beam generate attosecond pulses by a non-linear interaction with a medium, successive attosecond pulse produced in different laser cycles are emitted in different directions and, in appropriate conditions, can be spatially separated. This provides a scheme to generate, from a single laser pulse, a collection of angularly-separated beamlets each consisting of a single attosecond pulse. This is called an attosecond lighthouse (see figure 4).
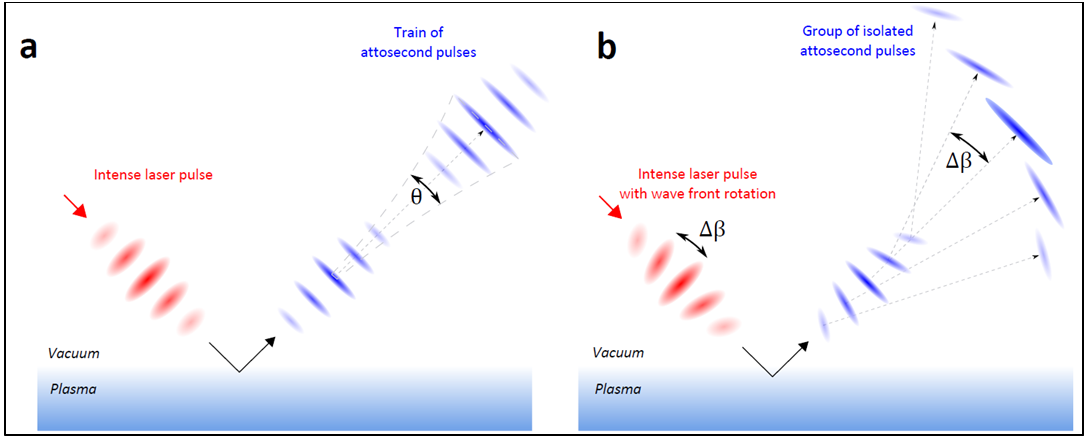
Figure 4: principle of attosecond lighthouses. a, When an intense few-cycle laser pulse interacts nonlinearly with a plasma mirror, the sub-cycle modulation of the temporal laser wavefronts is associated with the generation of a train of attosecond light pulses, which all propagate in a collimated beam along the direction normal to the laser wavefronts at focus. b, When the laser wavefronts are made to rotate in time at focus (wavefront rotation), each attosecond pulse of the train is emitted in a slightly different direction. When the wavefront rotation angle is greater than the divergence of an individual attosecond pulse, this scheme produces a manifold of spatially isolated and temporally synchronized attosecond pulses.
The first experimental demonstration of this effect was obtained in Salle Noire at LOA, in collaboration with the PCO group (see movie below) [Whe12]. The attosecond pulses were produced on plasma mirrors by CWE. It was then demonstrated in the case of attosecond pulses produced in gases, at much lower intensities, in collaboration with Prof. Corkum’s group in Ottawa [Kim13]. There has not been any experimental demonstration for attosecond pulses produced by ROM on plasma mirrors, because it requires a combination of very short laser pulse durations and ultrahigh intensities that is very difficult to achieve experimentally. But several implementations in gases have already been reported in different conditions [Zha15, Sil15] , leading in particular to the generation of broadband XUV pulses, potentially of attosecond duration, in the so-called ‘water window’ spectral range.
Movie of the attosecond lighthouse from plasmas : this movie shows the evolution of the spatial intensity profile of an attosecond lighthouse produced on a plasma mirror by CWE with 5 fs laser pulses, as the CEP of these pulses is scanned. The relative change in CEP is displayed in the upper right corner starting from an arbitrary absolute value. The arrows are reference markers introduced as an aid in visualizing the progression of the individual peaks.
Interaction with structured targets and transient plasma gratings
The interaction of UHI lasers with initially structured solid targets, and in particular with gratings, is an emerging topic, sometimes called UHI plasmonics. Evidence has recently been obtained, in particular in our group, that it allows for the coupling of the laser field with surface plasmons. This greatly enhances the absorption of laser energy by the target and lead to new acceleration mechanisms where electrons are directly accelerated by these surface plasmons, resulting in stronger and more energetic particle (ions, electrons) emissions [Cec13,Fed15].
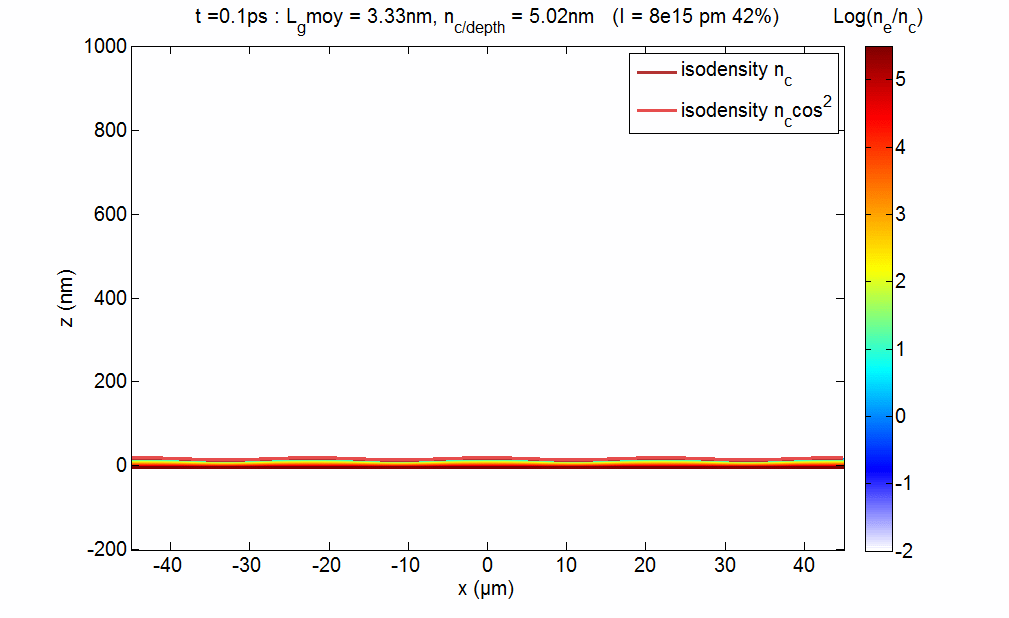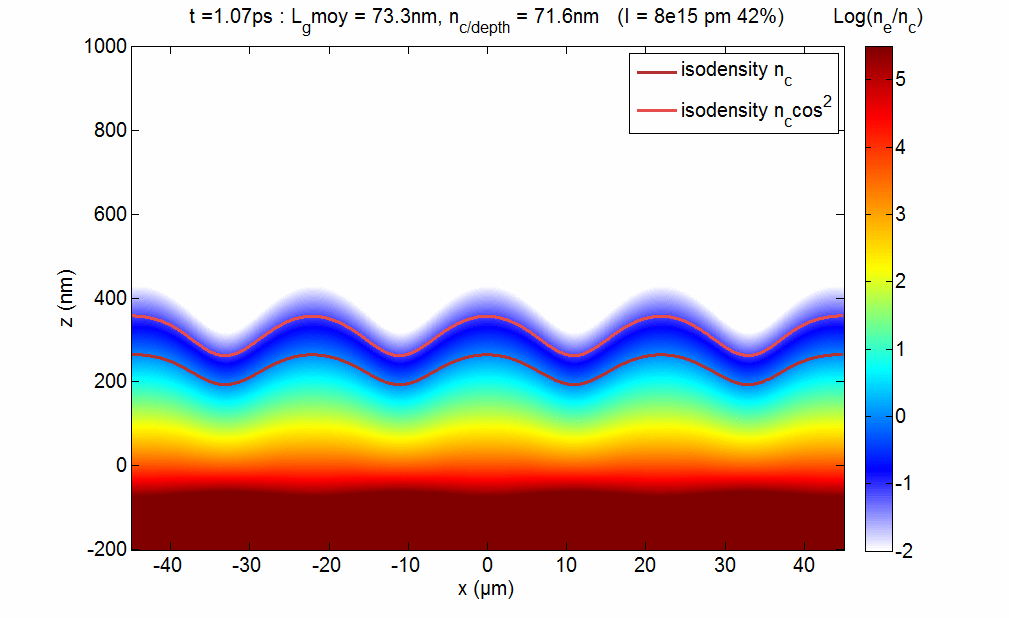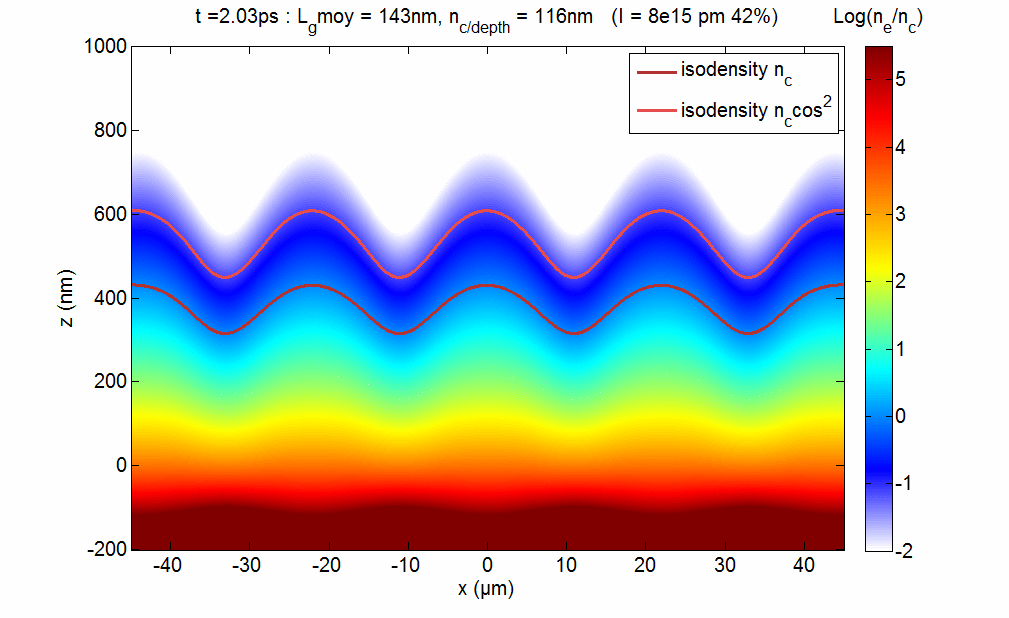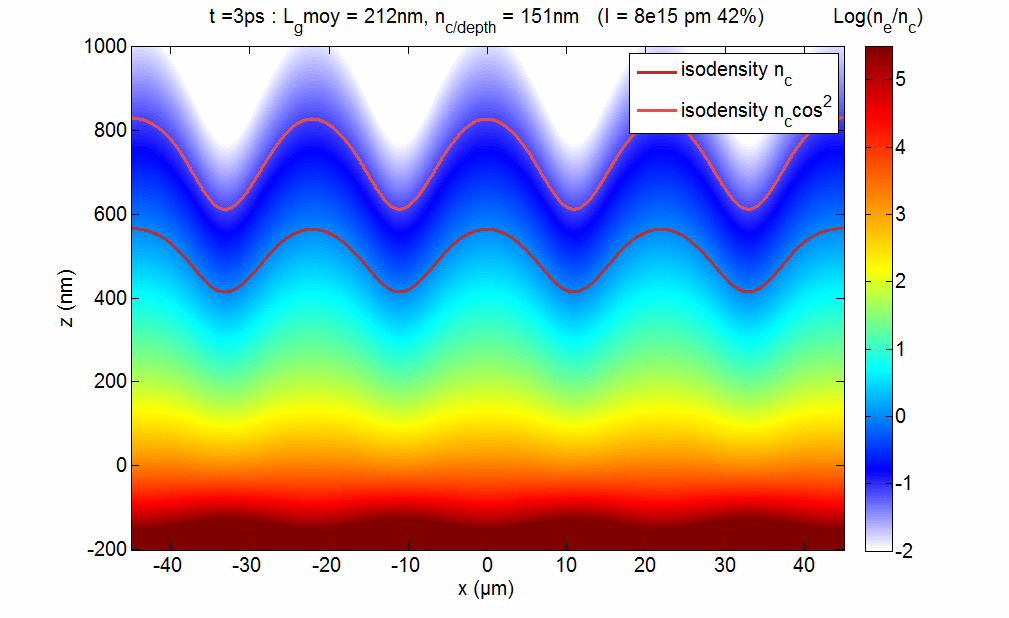
We have recently demonstrated how to optically create structured plasmas from initially flat surfaces. These so-called transient plasma gratings [Mon14] are created by initiating plasma expansion at the surface of a solid target with two prepulse that spatially interfere (see figure 5). These TPG will open new possibilities for UHI plasmonics, because their periodicity, depth and shape can be fully controlled optically. They can also be used to measure the E-field of the harmonic beam in the target plane by in situ ptychography [Leb15].
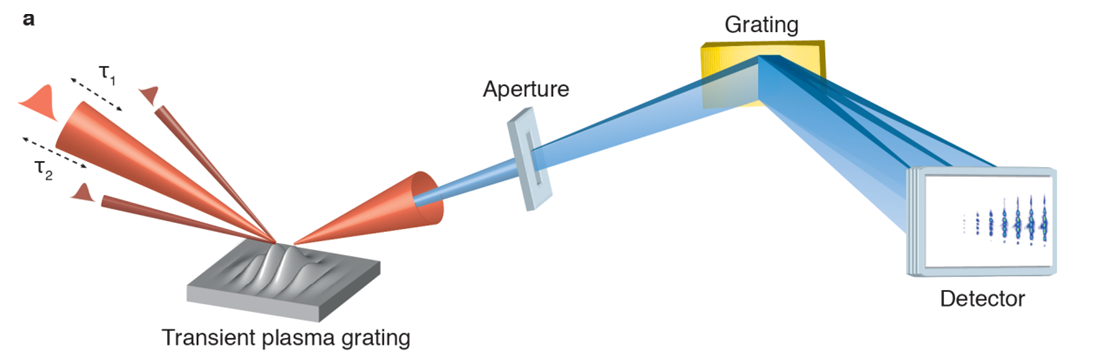
Figure 5 : Principle of transient plasma gratings. Two prepulse beams (I≈ 1016 W/cm2) cross at the surface of an initially solid target, which they strongly ionize. This initiates a plasma expansion with a velocity modulated in space due to the prepulse interferences. This leads to the growth of a transient plasma surface modulation, as illustrated by the hydrodynamic simulations displayed in movie ?? (gray scale: electron density ne, blue curve: isodensity surface g(x) corresponding to the critical plasma density nc). An ultraintense main laser pulse (25 fs, ≈1019 W/cm2) then interacts with this modulated plasma, and generates a beam of high-order harmonics in the specular direction. The diffraction pattern observed on this beam shows that transient plasma gratings can sustain ultrahigh laser intensities.
Plasma mirrors as injectors of electrons in UHI laser fields
Correlated with the harmonic emission and close to the direction of specular reflection, beams of relativistic electrons (≈ 10 MeV energies for I=3.1019 W/cm2, see Fig. 1) are also produced towards the vacuum. There have only been a limited number of experimental investigations of this electron emission in UHI conditions so far [Bra09,Mor09,Tia12], so that the complex underlying mechanisms are not well-understood yet [Gei06,Gei10].
We have recently revealed a crucial feature of this emission [The15]. Electrons are ejected out of the plasma surface in the form of attosecond bunches, with a relativistic velocity along the direction of the specularly reflected laser field. These electrons thus co-propagate with the reflected laser beam in vacuum, and can interact with it over distances on the order of the Rayleigh length. The spatial pattern observed on the electron beam (see figure 6) carries clear signatures of this interaction, and provides some of the most direct evidence so far of processes such as Vacuum Laser Acceleration (VLA, i.e. the direct acceleration of electrons by light in vacuum [Dod03], resulting in the bright peak in the electron beam, next to the specular direction) and relativistic ponderomotive scattering [Ques98] (resulting in the hole in the electron beam around the specular direction). By acting as injectors of electrons in the laser field, with measured charges in the 10 nC range, plasma mirrors thus open the way for the first time to the investigation of the dynamics of free relativistic electrons in ultraintense laser fields. This is a subject of high fundamental interest that has motivated considerable theoretical work in the last decades (e.g. [Har95,Esa95,Yu00,Stu01,Sal02,Pan02,Dod03, Mal03,Var06], but which had so far remained inaccessible experimentally.
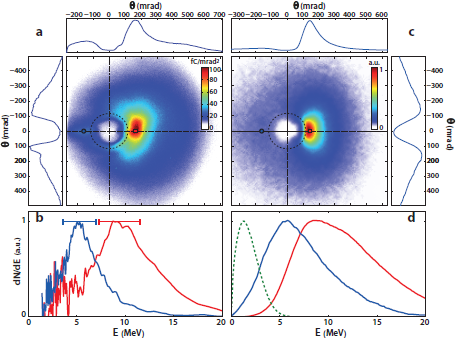
Figure 6: Experimental evidence of vacuum laser acceleration. Panel a) shows a typical experimental angular distribution of electrons emitted from plasma mirrors into the vacuum. It consists of a broad emission cone (blue disk), which is strongly modulated by two main patterns. One is a well-defined hole (in white) around the reflected laser beam (whose size and position in the detection plane are indicated by the dashed circle), due to the ponderomotive scattering of electrons after their ejection from the plasma mirror. The other is a bright peak (in red), right on the edge of this hole, due to Vacuum Laser Acceleration of a fraction of these electrons. Panel b) shows the electron spectra measured at two different locations in the beam. These locations are indicated by the blue circle and the red square in panel a), that respectively correspond to the blue and red curves of panel b). Panel c) and d) show the same quantities, now obtained from numerical simulations based on a 3D test particle model. The dashed curve in panel d) shows the initial electron energy distribution used in this model.
[Bor12] Borot et al, Nature Physics 8, 416-421 (2012)
[Bra09] Brandl et al, Phys. Rev. Lett. 102, 195001 (2009)
[Cec13] Ceccotti et al, Phys. Rev. Lett. 111, 185001 (2013)
[Dod03] Dodin & Fisch, Phys. Rev. E 68, 056402 (2003)
[Dou04] Doumy et al, Phys. Rev. E 69, 026402 (2004)
[Kah13] Kahaly et al, Phys. Rev. Lett. 110, 175001 (2013)
[Kim13] Kim et al, Nature Photonics 7, 651–656 (2013)
[Esa95] Esarey et al, Phys. Rev. E 52, 5443 (1995)
[Fed15] Fedeli, submitted to Phys. Rev. Lett. (2015)
[Gei06] Geindre et al, Phys. Rev. Lett. 97, 085001 (2006)
[Gei10] Geindre et al, Phys. Rev. Lett. 104, 135001 (2010)
[Har95] Hartemann et al, Phys. Rev. E 51, 4833 (1995)
[Leb15] A. Leblanc et al, submitted (2015)
[Lev07] Lévy et al, Optics Letters 32, 3 (2007)
[Mal03] Maltsev&Ditmire, Phys. Rev. Lett. 90, 053002 (2003)
[Mon04] Monot et al, Optics Letters 29 , 893-5 (2004)
[Mon14] Monchocé et al, Phys. Rev. Lett. 112, 145008 (2014)
[Mor09] Mordovanakis et al, PRL 103, 235001 (2009)
[Pan02] Pang et al, Phys. Rev. E 66, 066501 (2002)
[Que06] Quéré et al, Phys. Rev. Lett. 96, 125004 (2006)
[Que08] Quéré et al, Phys. Rev. Lett. 100, 095004 (2008)
[Ques98] Quesnel &. Mora, Phys. Rev. E 58, 3719 (1998)
[Sal06] Salamin et al, Phys. Rev. A 73, 043402 (2006)
[Sil15] Silva et al, Nature Comm. 6, 6611 (2015)
[Stu01] Stupakov et al, Phys. Rev. Lett. 86, 5274 (2001)
[Tha07] Thaury et al, Nature Physics 3, 424 - 429 (2007)
[Tha08] Thaury et al, Nature Physics 4, 631 (2008)
[Tha10] Thaury & Quéré, J. Phys. B. 43, 213001(2010)
[The15] Thévenet et al, submitted to Nature Physics
[Tia12] Tian et al, Phys. Rev. Lett. 109, 115002 (2012)
[Var06] Varin & Piché, Phys. Rev. E 74, 045602 (2006)
[Vin12] Vincenti & Quéré, Phys.Rev.Lett. 108, 113904 (2012)
[Vin14] Vincenti et al, Nature Communications 5, 3403 (2014)
[Whe12] Wheeler et al, Nature Photonics 6, 829–833 (2012)
•  Interaction laser-matière ›
Interaction laser-matière ›  Interaction laser-matière en champ fort
Interaction laser-matière en champ fort
• Interactions, Dynamics and Lasers Laboratory (LIDYL) - CEA-CNRS and Paris Saclay University • Laboratoire Interactions, Dynamiques et Lasers (LIDYL) - CEA-CNRS et Université Paris Saclay
• Physic at High Intensity • Physique à Haute Intensité / High intensity Physics













