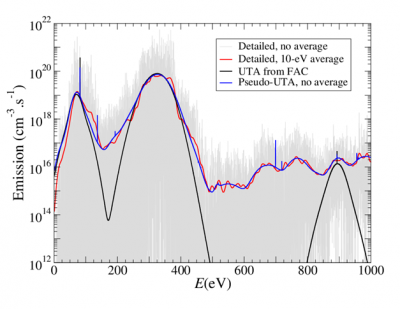
Figure 1 : Detailed M1 and UTA or pseudo-UTA emission of a W54+ plasma.The gray curve is the emission calculated with the FAC detailed code. The red curve is obtained by convoluting the gray curve with a Gaussian profile of 10-eV FWHM in order to simulate an experimental broadening and facilitate comparisons. The black curve results from the UTA calculation using the inline formulas in the FAC code. The blue curve is obtained by a definition of pseudo-UTA [Na2017].
The analysis of the spectral properties of warm dense plasmas such as those present in stellar atmospheres, inertial confinement fusion devices or laser-plasma experiments can involve two types of interpretation. On the one hand, the detailed or “fine structure” approach is based on the determination of all the energy levels obtained by diagonalization of the atomic Hamiltonian, after choosing an adapted set of configurations. On the other hand, the averaged or “statistical” approach consists in characterizing the absorption and emission structures — between two non-relativistic or relativistic configurations — by some global values such as the average energy, the variance of the transition energy, etc. These quantities which are averages of integer powers of the transition energy are called “moments”. The interest of these first moments is that i) their knowledge is sufficient in a large number of cases to describe a set of hundreds or thousands of lines ii) their analytical determination is possible for transitions involving one or more active electrons. These averaging techniques, based on second-quantization techniques and tensor algebra, were developed by Bauche et al [Bauche1979, Bauche1988].
As well as it is possible to obtain analytically the first moments of the transition energy between two configurations, similar techniques allow us to calculate the mean energies and the centered averages of the successive powers of the energy for all levels of a configuration. Concerning the contribution of electronic repulsion to energy, the general formulas were published several years ago up to the 3rd-order moment [Bauche2015, Kucas1993]. At higher orders the formulas become very cumbersome. However, concerning the spin-orbit Hamiltonian, it is possible to give analytical expressions of the moments of any order [Na2016]. The use of these formulas makes it possible to calculate the moments of order 2 and 3 in any configuration. For example we have been able to verify that the formulas giving the moments of order 2 and 3 in the d6 configuration of Au55+ are in very good agreement with a numerical computation using the Cowan code [Na2016]. These spectroscopic quantities are particularly useful in the study of highly charged ions.
We have also investigated the case of magnetic dipole M1 transition arrays. This type of transition tends to become non-negligible with respect to electrical dipole transitions for ions of high net charge. This is the case of the tungsten ions present in the plasmas of divertor of tokamaks such as ITER. This study was conducted numerically using the FAC code. The formulas for the M1 transition beams have recently been derived and implemented in the code. However, our analysis has shown that the formulas for various types of transitions arrays are missing, namely the transitions internal to a configuration and the transitions involving several electrons [Figure 1]. Using a definition of pseudo-arrays [Na2017b] — the moments of which are obtained by a numerical average on the detailed lines and not by analytical expressions — we were able to find a good agreement between the detailed spectra and pseudo-UTA as shown in Figure 1.
References :
- [Bauche1979] C. Bauche-Arnoult, J. Bauche, and M. Klapisch, Phys. Rev. A 20, 2424 (1979).
- [Bauche1988] J. Bauche, C. Bauche-Arnoult, and M. Klapisch, Adv. At. Mol.Phys. 23, 131 (1988).
- [Bauche2015] J. Bauche, C. Bauche-Arnoult, and O. Peyrusse, Atomic Properties in Hot Plasmas (Springer Verlag, Berlin, 2015).
- [Kucas1993] S. Kucas and R. Karazija, Phys. Scr. 47, 754 (1993).
- [Na2016] Xieyu Na and M. Poirier, Phys. Rev. E 94, 13206 (2016).
- [Na2017a] Xieyu Na, “Spectroscopic study of highly ionized plasmas: detailed and statistical approaches” (Thèse d’Université, Paris-Sud, 2017).
- [Na2017b] Xieyu Na and M. Poirier, “Analysis of magnetic-dipole transitions in tungsten plasmas using detailed and configuration-average descriptions”High Energy Density Phys. 23 200 (2017).


