Codes particulaires
De par sa brièveté et son intensité, l'interaction d'une impulsion laser avec la matière peut être suivie de manière précise grâce aux outils numériques que ce début de siècle met à notre disposition. Les impulsions laser, durant quelques dizaines de période du champ laser, interagissant avec des cibles solides, de quelques longueurs d'onde laser d'épaisseur, peuvent être simulées grâce à des outils numériques particulièrement performants, à savoir les codes particulaires. Ces codes calculent numériquement l'évolution de la densité des particules en présence, électrons et ions, dans l'espace des phases (position, impulsion) couplée à l'évolution des champs électromagnétiques extérieurs ou auto-générés. Le modèle sous-jacent consiste donc en un couplage des équations de Vlasov, une par espèce de particules, et des équations de Maxwell.
Ces codes sont donc capables de capturer une physique très riche, car relevant d'un modèle cinétique de la matière bien supérieur au modèle hydrodynamique usuel pour suivre des écoulements, et de le faire de façon efficace, en ne maillant que les dimensions spatiales pour les champs et en gérant la dynamique des espaces des phases par des macro-particules. Cette approche lagrangienne de l'espace des phases, qui conduit à la présence de macro-particules là où la matière est dense, évite l'utilisation de mailles en impulsion où la densité de matière resterait faible. Cette physique et cette gestion font que, depuis leur apparition dans les années 60, ces codes particulaires ont tenu et tiennent le haut du pavé de la simulation des plasmas. Ils sont aptes à représenter les phénomènes ondulatoires dans leur vie complète, propagation linéaire, couplage d'ondes faiblement non-linéaires, comportement fortement non-linéaire avec cambrure des ondes, profil de choc et enfin déferlement avec l'accélération associée des particules.
Avec 1021 W/cm2 accessibles actuellement dans le monde (pratiquement 1020 à Saclay), des électrons au GeV (impulsion pe/mec <102) et des ions à 100 MeV (impulsion pi/ mic <0.3) sont détectés lors de l'impact laser sur la cible. Au moins pour les électrons, l'équation de Vlasov est donc traitée dans une approche relativiste. Ce modèle est capable de suivre des plasmas non collisionnels, où la longueur de Debye est beaucoup plus grande que la distance inter-particule elle même plus grande que la distance de Landau. La réalité fait que l'interaction laser-matière débute par une phase d'ionisation et une corrélation entre particules via des collisions binaires. Ces deux phénomènes relevant d'un modèle à N corps quantique ou classique n'ont que très peu été retenus dans ces codes particulaires, fondamentalement associés à des comportements non-collisionnels modélisés par l'équation de Vlasov. Mais depuis le début de cette décennie, progrès informatiques aidant, des modèles ont fleuri en vue d'intégrer cette physique aux codes particulaires, via une technique Monte-Carlo : au vu d'une probabilité actualisée d'ionisation et de collisions, fonction du champ électrique et de la densité électronique locale au sein d'une maille, des atomes/ions sont ionisés et des électrons/ions voient leur trajectoires déviées. Par cette technique Monte-Carlo, la physique associée à des échelles de quelques nanomètres, relevant de "l'infra-Debye" si l'on peut s'exprimer ainsi, est prise en compte ; la méthode particulaire avec ses macro-particules de taille finie gère "le supra-Debye".
Contraintes informatiques
Un simple PC actuel cadencé à 2 GHz permet de traiter chaque macro-particule, via 1 composante de position et 3 composantes d'impulsion, en moins d'une microseconde. Le passage en 2D et 3D spatial nécessite un nombre de macro-particules plus conséquent avec un traitement légèrement plus long mais le temps donné par macro-particule est caractéristique des contraintes actuelles. Grossièrement, en 1D, une cible de 0.8 µm d'épaisseur, de densité électronique initiale (liés +libres) égale à 1023 cm-3 simulée pendant 100 fs d'une impulsion à la longueur d'onde 0.8 mm demande 6 104 macro-particules, 3 104 pas de temps et environ 30 minutes sur un PC, pour le traitement Vlasov-Maxwell seul. Avec l'ionisation et collisions, ce temps est doublé. Le passage au 2D sur une largeur de la tache focale de 10 longueurs d'onde demande 103 plus de temps. Le passage sur calculateur à multiprocesseurs parallèles est obligatoire : dans le cadre d'une parallélisation parfaite, sur 100 processeurs, la simulation prend environ 7 h. Le 3D serait, on le voit, beaucoup trop lourd pour une cible solide. En revanche, la simulation 3D d'un jet de gaz est abordable, la longueur de Debye étant beaucoup plus grande. Avec une maille et un pas de temps respectivement de 0.05 µm et 0.2 ps, la simulation de la propagation sur environ 100 µm serait de 4 h.
Pour résumer, l'environnement informatique de 2008 permet d'utiliser les codes particulaires en géométrie spatiale 1D pour des études paramétriques et test de modèles, en 2D sur cible solide, et en 3D sur cible gazeuse. Notons que le raccourcissement spectaculaire des impulsions laser en deçà des 50 fs facilite la vie du simulateur, comparativement au démarrage de cette aventure UHI en 1990 à Saclay où les impulsions duraient de 0.3 à 1 ps.
Code EUTERPE
Les quelques points qui suivent rapportent le travail numérique réalisé récemment sur le code EUTERPE, simulant tous les comportements mentionnés ci-dessus en géométrie spatiale 1D. Ce code créé au CEA/DAM par G. Bonnaud a été régulièrement complété et amélioré et a été (ou est) quotidiennement utilisé tant au CEA/DSM/IRAMIS et CEA/DAM/Bruyères qu'aux laboratoires LULI à Palaiseau et CELIA à Bordeaux. Il a la particularité de pouvoir simuler l'interaction oblique d'une onde plane avec une cible, évitant le passage au 2D beaucoup plus coûteux. Depuis des années, ce code a été le support ou l'origine de nombreuses publications depuis 1985, tant dans le domaine de la fusion contrôlé inertielle que dans celui des impulsions laser d'ultra-haute intensité.
La formation des futurs physiciens est capitale. L'INSTN par son positionnement au sein de l'organisme CEA a pour mission de diffuser le savoir associé aux recherches réalisées au CEA. A destination des stagiaires de master ("Optique,matière,plasma", "Sciences de la fusion", ...), doctorants, et nouveaux venus dans cette thématique, un site INSTN accessible en intranet CEA fournit un ensemble de 300 pages rassemblant les principes de la simulation particulaire, la description du code EUTERPE, les tests sur les différents paramètres numériques et l'illustration par EUTERPE de différents processus de physique des plasmas (cf. site web \\instna\public\PUBLIC_GB\EUTERPE\euterpe.html).
Auto-chauffage numérique
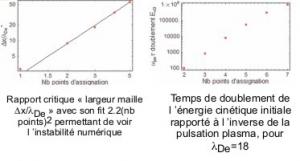
Une des caractéristiques fâcheuses des codes particulaires se trouve dans ce qui s'appelle le bruit numérique, contribuant à donner aux champs internes au plasma des amplitudes au dessus de la réalité. De plus, ce bruit croît via l'auto-chauffage du plasma, qui résulte d'une instabilité de nature numérique associée aux grandes mailles (grandes en comparaison avec la longueur de Debye λDe). Dans un code particulaire, les macro-particules ne sont pas ponctuelles mais sont étalées sur une ou plusieurs mailles, le prix étant la complexité et le coût numérique engendré. Le rapport qualité/temps fait que, de manière habituelle, les codes particulaires utilisent un étalement sur 2 nœuds de maillage (méthode dite PIC ou "Particle-in-cell"). Depuis 1 ½ an, EUTERPE peut désormais fonctionner jusqu'à 8 nœuds. La courbe ci-dessous rapporte la réduction spectaculaire de l'auto-chauffage numérique et du bruit numérique. 4 points d'assignation sont suffisants et sont devenus d'utilisation standard dans toutes nos simulations. Par cette amélioration, le nombre de macro-particules peut être divisé d'un facteur 10 au minimum par rapport au cas PIC, rendant encore plus facile l'utilisation de ce code.
Ionisation
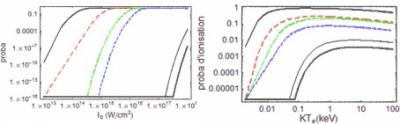
Ci-dessous la probabilité d'ionisation du carbone sur un pas de temps de 0.2 fs : à gauche, par effet tunnel (induit par l'éclairement laser incident) et à droite, par effet collisionnel e-i (induit par la température électronique) (de gauche à droite C → C+ (noir), C+ →C2+ (rouge), ... jusqu'à C 5+ → C 6+ )
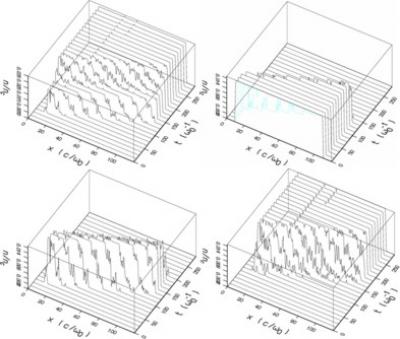
Ci-dessous une cible de carbone pur éclairée par un éclairement 1016 W/cm2 à la longueur d'onde λ0 = 1 μm. La densité de la cible se mesure par la densité volumique d'électrons (initialement liés) rapportée à la densité nc d'électrons libres minimale interdisant la propagation de la longueur d'onde dans le plasma (= 1021/λcm-3 avec λ0 (μm)). Ici la densité d'atomes est de 0.1 nc/6, donnant ne/nc = 0.1. Au départ, l'onde se propage comme dans le vide, les électrons liés n'ayant aucun rôle. Ci-dessous les différents états de charge observés au cours du temps en tout point du plasma (l'onde laser se propage dans le sens des x croissants). Les ions C+ sont visibles transitoirement ; ils sont ionisés en C2+. La densité C3+ de dépasse pas 0.001 nc ; C4+ à C6+ sont invisibles.
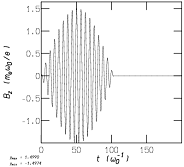
Le plasma ci-dessus était transparent. Une cible de densité plus élevée (transparente à faible éclairement laser) devient opaque à haut éclairement : c'est le principe du miroir plasma. Ci-dessous, l'état de charge résolu en espace d'une cible de plastique (C et H de densités atomiques respectives 20 nc et 60 nc), donnant une densité d'électrons ne/nc = 180. L'impulsion laser éclairant la cible a une durée totale de 56 fs avec un éclairement maximal de 3x1018 W/cm2. Le profil temporel du champ magnétique de l'onde incident est ci-dessous :
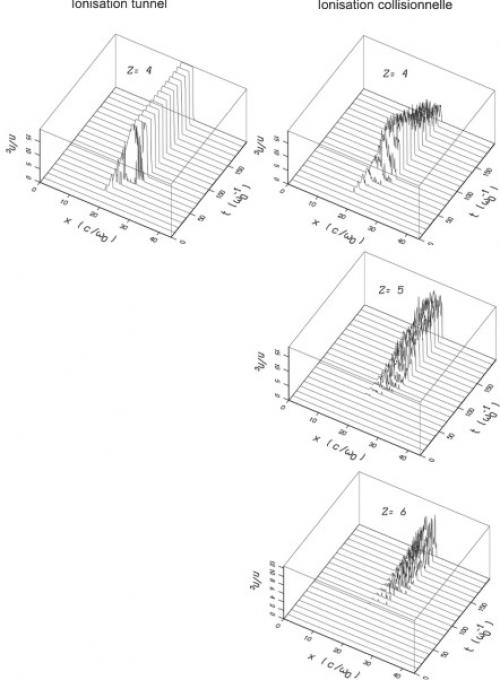
L'évolution spatio-temporelle de la densité de C4+ montre que l'ionisation limitée au seul effet tunnel (à gauche) ionise la cible à C4+ , alors que l'ensemble "tunnel + collisions" (à droite) permet aux ions C4+ de s'ioniser en C5+ et C6+ , en cohérence avec les probabilités présentées ci-dessus.
• Service des Photons Atomes et Molécules
• Groupe édifices nanométriques • Laboratoire Francis Perrin • Matière sous conditions extrêmes • Matter under Extreme Conditions • Support et Lasers à Impulsions courtes / Support and short pulse lasers